本章练习答案
1:用迭代法求方程x5-4x-2=0在![]() 的最小正根,使敛代误差不超过
的最小正根,使敛代误差不超过![]() 。
。
解:建立迭代格式
![]()
![]() (可任取1,2之间的值)
(可任取1,2之间的值)
![]() 1.431 0
1.431 0 ![]() 1.505 1
1.505 1
![]() 1.516 5
1.516 5 ![]() 1.518 2
1.518 2
![]() 1.5185
1.5185
![]()
![]() 取
取![]() 1.5185
1.5185
2:应用牛顿法试导出一个求![]() 迭代求解公式。
迭代求解公式。
解:显然![]() 为方程
为方程![]() 的根,于是有迭代法
的根,于是有迭代法![]()
3:利用适当的迭代格式证明: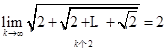
证明:考虑迭代格式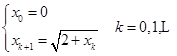
则:![]() ,
,![]() ,
,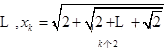
![]() ,当
,当![]() 时,
时,![]() ;
;![]() ,因此迭代收敛。
,因此迭代收敛。
4:迭代法![]() 收收敛于
收收敛于![]() ,此迭代式是 阶收敛
,此迭代式是 阶收敛
解:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,二阶收敛。
,二阶收敛。
5:![]() 要使迭代式
要使迭代式![]() 局部收敛到
局部收敛到![]() ,则
,则![]() 的取值范围是 。
的取值范围是 。
解:![]() ,迭代式收敛即要求
,迭代式收敛即要求![]()
6: 求![]() 的根的牛顿迭代格式是 。
的根的牛顿迭代格式是 。
解:![]() (牛顿迭代式)
(牛顿迭代式)
7:应用牛顿迭代法求方程![]() 的根
的根![]() 的近似值,其收敛阶为 。
的近似值,其收敛阶为 。
解:![]() 为方程的重根,因此,收敛阶为1。
为方程的重根,因此,收敛阶为1。
8: 证明:对任何初始值![]() ,由迭代式
,由迭代式![]() 所产生的序列
所产生的序列![]() 都收敛于方程
都收敛于方程![]() 的根。
的根。
证明:![]() ,则
,则![]()
![]() 先考虑区间
先考虑区间![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,故迭代式
,故迭代式![]() 所产生的序列均收敛。
所产生的序列均收敛。
![]() 对任何初始值
对任何初始值![]() ,有
,有![]() ,将
,将![]() 看成新的迭代初值,则由
看成新的迭代初值,则由![]() 知其必收敛。
知其必收敛。
9:试确定常![]() 使迭代公式
使迭代公式![]() 产生的序列
产生的序列![]() 收敛到
收敛到![]() ,并使其收敛阶尽可能高。
,并使其收敛阶尽可能高。
解:迭代函数![]() ,根据高阶收敛定理,要使迭代序列收敛的阶尽可能高,应使
,根据高阶收敛定理,要使迭代序列收敛的阶尽可能高,应使![]() ,
,![]()
由![]() 得:
得:![]() ,即
,即![]() ;
;
由![]() 得:
得:![]() ,即
,即![]()
由![]() 得:
得:![]() ,即
,即![]()
综上可得![]() 满足方程
满足方程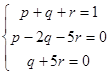 ,从而
,从而![]() ,而且
,而且![]() ,故迭代公式具有三阶收敛性。
,故迭代公式具有三阶收敛性。
10: 用弦截法求方程x3-x2-1=0,在x=1.5附近的根,取![]() 。保留5位小数点计算至
。保留5位小数点计算至![]() 。
。
解 f(x)= x3-x2-1,f(1)=-1,f(2)=3,有根区间取[1,2]。
迭代公式为: ![]() (k =1,2,…)
(k =1,2,…)
![]()
![]() 1.37662
1.37662
![]() 148881
148881
![]() 146348
146348
![]() 1.46553
1.46553
取![]() 1.46553,f(1.46553)»-0.000145
1.46553,f(1.46553)»-0.000145
11: 对![]() 为
为![]() 的一个不动点,验证
的一个不动点,验证![]() 的迭代对
的迭代对![]() 不收敛,但改用Aitken方法却是收敛的。
不收敛,但改用Aitken方法却是收敛的。
证明:由于![]() ,当
,当![]() 时,
时,![]() ,且有
,且有![]() 在
在![]() 与0之间,
与0之间,
若![]() ,
,![]() 时,迭代不收敛。
时,迭代不收敛。
若改用Aitken方法,可得![]() ,据局部收敛定理知,知其局部收敛于不动点0。
,据局部收敛定理知,知其局部收敛于不动点0。
12:设![]() ,利用Newton法求平方根
,利用Newton法求平方根![]() ,并证明迭代公式对
,并证明迭代公式对![]() 均具二阶收阶性。
均具二阶收阶性。
解:令![]() .
. ![]() 即
即![]() 的根,则Newton公式为:
的根,则Newton公式为:![]()
无论![]() 或
或![]() 时均有:
时均有: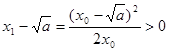 ,即
,即![]()
假设任意![]() ,
,![]() ,
,![]() ,即从
,即从![]() 开始
开始![]() ,且
,且 ![]() ,
,![]() 从
从![]() 起是一个单调递减有下界的序列,由数列收敛定理知{
起是一个单调递减有下界的序列,由数列收敛定理知{![]() }有极限
}有极限![]() .令
.令![]() 可得
可得![]() ,这就说明了只要
,这就说明了只要![]() ,迭代总收敛到
,迭代总收敛到![]() ,且是二阶收敛.
,且是二阶收敛.