1：用迭代法求方程x5－4x－2＝0在的最小正根，使敛代误差不超过。

2：应用牛顿法试导出一个求迭代求解公式。

3：利用适当的迭代格式证明：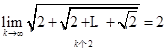

4：迭代法收收敛于，此迭代式是         阶收敛

5：要使迭代式局部收敛到，则的取值范围是             。

6: 求的根的牛顿迭代格式是                        。

7：应用牛顿迭代法求方程的根的近似值，其收敛阶为        。

8: 证明：对任何初始值，由迭代式所产生的序列都收敛于方程的根。

9：试确定常使迭代公式产生的序列收敛到，并使其收敛阶尽可能高。

10: 用弦截法求方程x3－x2－1＝0，在x=1.5附近的根，取。保留5位小数点计算至。

11:　对为的一个不动点，验证的迭代对不收敛，但改用Aitken方法却是收敛的。

12：设，利用Newton法求平方根，并证明迭代公式对均具二阶收阶性。