5.6 迭代法的收敛阶和Aitken加速方法

在关于迭代法定理5的假设条件下，且，由中值公式有

           （5.6.1）

其中，在与之间，且由，于是。又由（5.6.1）式及连续性，故误差有关系

                （5.6.2）

由定理6可知，关于求解方程牛顿法产生的误差有关系

    　          （5.6.3）

一般情况下，设有方程及迭代过程

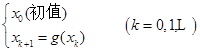     　　　　　　　　（5.6.4）

且设收敛于。

如果误差有关系

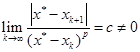                （5.6.5）

其中，为实数且，为正常数，称迭代过程为阶收敛，当时（且要求）称迭代过程为线性收敛，当时称迭代过程为超线性收敛，当时称迭代过程为二次收敛（或为平方收敛）。

如果一迭代过程为阶收敛时，式（5.6.5）表示当充分接近根时有

        　　       （5.6.6）

式（5.6.6）反映了在接近收敛于过程中，每迭代一次近似解误差的缩减速度，当数值不大时，近似解误差下降速度主要取决于式（5.6.6）中的幂次。越大，收敛于速度就越快，于是可以作为衡量迭代法收敛速度的一种度量。因此值的大小是衡量一个迭代过程优劣的标志之一。

于是，一般迭代法,当时迭代过程为线性收敛（由定理5及（5.6.2）式，）。牛顿法具有二阶收敛（由定理6及（5.6.3）式，）。牛顿法在接近收敛过程中，近似根的误差将是二次方地下降，因此牛顿法在单根邻近具有较快的收敛速度。但牛顿法对初值要求比较苛刻。初值选取不好，牛顿法可能不收敛。当为的二重根时，则牛顿法为线性收敛。

正割法收敛阶为(由(5.5.2)式)是超线性收敛，抛物线方法收敛阶为(由(5.5.9)式)。

对于收敛较慢的数列(例如，由迭代过程产生)，一个补救的方法是采用加速公式。

设有　　，且  

于是

                  (5.6.7)

则能由，，用下述方程确定，事实上，由式（5.6.7）有

解出即得

         (5.6.8)

上式说明，当式（5.6.7）得到较好的满足时，则是近似值的很大的改进。于是，由数列可定义一新的数列。

定义3

            (5.6.9)

且序列可能比更快的收敛于。这种由给出的序列（收敛较慢）来计算新序列的方法称为Aitken加速法。

当迭代过程收敛很慢时，一般可用Aitken加速法，但有时Aitken法加速可能失败，如当起伏很大，初值和根有较很大的距离时，Aitken加速就可能失败。

将Aitken加速法用于迭代法就产生了被称为斯蒂芬森（Steffensen）法。

设有方程,为初值。

（1）迭代

           　　 （5.6.10）

（2）加速

       　　　　　（5.6.11）

Steffensen方法计算步骤：设方程，

（1）输入初值（最大迭代次数），（精度要求）；

（2）对于。

 

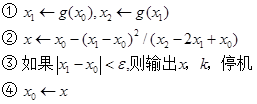
（3）输出：（“method failed after No iterations,No=”No）

例14 设有方程，试用Steffensen方法求内方程根的近似值。

解   迭代过程，，计算到，方法的精确解为。。现用Steffensen法加速（即式（5.6.10）和（5.6.11）），结果见表5—13，且，加速效果较好。

表5—13