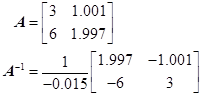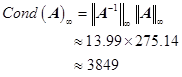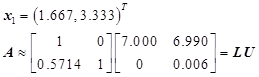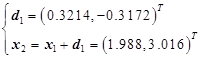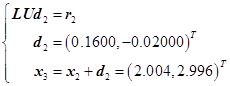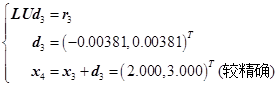内容导入

对于线性方程组,假设为非奇异矩阵，为方程组的解。在应用问题归结为求解方程组时，其系数矩阵和可能有某些观测误差，或者，是计算的结果，从而包含有舍入误差。研究数据或的误差对方程组解的影响，引入病态方程组。

设有方程组，其中为非奇异阵，且若方程组不过分病态，又设用高斯消去法（或部分选主元消去法）求得计算解（精度不高），我们希望获得方程组高精度的解，一般可采用下述的迭代改善法，用来改善的精度。

教师解析

内容简介

病态方程组：方程组常数项分量只有微小变化，而方程组的解有较大的变化，这样的方程组就是病态方程组。

常数项b的微小误差对解的影响：

（1）为精确解，为非奇异矩阵；

（2）且设

则有。

扰动对解的影响：

（1）设，其中为非奇异矩阵，为精确解；

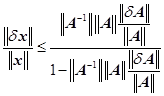（2）设，且设，则的微小误差引起解的相对误差有估计式，且说明，如果数越大，的微小相对误差可能引起的解的相对误差就愈大，因而数的大小刻画了方程组的解对问题数据（或）的灵敏程度。

通过矩阵的条件数定义病态方程组：

设，其中为非奇异矩阵，如果（相对大的条件数）称为病态方程组，如果相对的小，称为良态方程组。的条件数愈大，方程组病态愈严重。

迭代改善法：设，为非奇异阵且方程组不是过分病态。用数组保存元素，用数组保存三角矩阵，用记录行交换信息，用存放及，用数组存放或。

(1)用高斯消去法（或列主元消去法）计算近似解且实现分解(或)。   

(2)对于

 ①计算（双精度）；

 ②求解（或）；（解两个三角形方程组）

 ③计算。

可以用 控制迭代。

边学边练

练习题1 设，试计算 。

练习题2 用迭代改善法解