1 用顺序消去法解线性方程组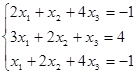

2：，当满足            时，顺序高斯消元能进行到底；当满足            时，方程组可用顺序高斯消去法求解。

3：以二元线性方程组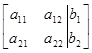为例，说明Gauss消去法求解时为什么要选主元？

4：设为阶非奇异矩阵，且有三角分解，其中为单位下三解阵，为上三角阵，求证：的所有顺序主子式均为零。

分析：因为要证的所有顺序主子式均不为零，故把按分块的形式写出比较好，再由的非奇异性即可推证。

5：非奇异矩阵不一定都有分解。

6：取初始向量X(0)=(0，0，0)T，用雅可比迭代法求解线性方程组

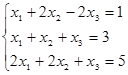
7：用高斯列主元消去法解线性方程组

作第1次消元后的第2，3个方程分别为                              。

8：用高斯－赛德尔迭代法解线性方程组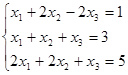的迭代格式中＝

              (k=0，1，2，…)

9：已知方程组

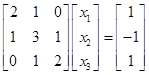
（1）证明高斯－塞德尔法收敛；

（2）写出高斯－塞德尔法迭代公式；

（3）取初始值，求出。

10：当(   )时，线性方程组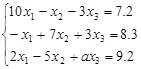的迭代解一定收敛。

(A) a<7  (B) a=4  (C) <4  (D) ½a½>7

11：用紧凑格式对矩阵进行的三角分解，则＝（ ）

A．1    B．       C．–1        D．–2

12：，证明是的范数

13：，          ，          。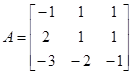

14： ，则A的谱半径            

15：设为阶非奇异阵，表示矩阵的任何一种算子范数，试证：

16：向量，是不是一种向量范数？是不是一种向量范数？

17：，证明：

18：试证明G-S迭代矩阵至少有一个个特征值为0

其中。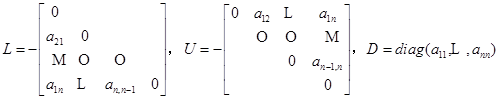

19：给定线性方程组，，用迭代公式求解，间取什么实数可使迭代收敛？什么可使迭代收敛最快？

20：讨论用Jacobi法和Gauss-Seidel方法解方程组时的收敛性，如果收敛，并比较哪种方法收敛较快，其中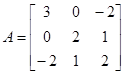

21：设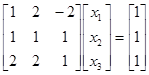，试求Jacobi及G-S法迭代矩阵

22：设为阶非奇异矩阵，求证：的解总能通过GS法得到。