当前位置:课程学习>>第七章>>知识讲解>>视频课堂>>知识点五
知识点五:算法的数值稳定性
内容导入
微分方程的数值解法是通过离散化将微分方程转化为差分方程(代数方程)来求解的,而在差分方程的求解过程中,存在着各种计算误差,这些计算误差如舍入误差等引起的扰动,在误差传播过程中,可能会大量积累,以至于“淹没”了差分方程的真解。
教师解析
内容简介
算法的稳定性:当在某节点![]() 上的
上的![]() 值有大小为δ的扰动时,如果在其以后的各节点
值有大小为δ的扰动时,如果在其以后的各节点![]() 上的
上的![]() 值产生的偏差都不大于δ,则称这种方法是稳定的。
值产生的偏差都不大于δ,则称这种方法是稳定的。
(1) 阿达姆斯隐式方法的稳定区域都比同阶的显示方法的大,只是隐式方法最大的优点;
(2) ![]() 越大(即步数、阶数越大)时稳定区域就越小,只有隐式欧拉方法才是绝对稳定的。
越大(即步数、阶数越大)时稳定区域就越小,只有隐式欧拉方法才是绝对稳定的。
算法的收敛性:微分方程在离散为差分方程来求解,当步长![]() 时,存在着差分方程的解
时,存在着差分方程的解![]() 能否收敛到微分方程的准确解
能否收敛到微分方程的准确解![]() 的问题。对于任意节点
的问题。对于任意节点![]() ,当
,当![]() (同时
(同时![]() )时,
)时,![]() 都能趋向于准确解
都能趋向于准确解![]() 的算法,称为是收敛的,否则称为不收敛。
的算法,称为是收敛的,否则称为不收敛。
边学边练
练习题 分别用二阶Adams显式和隐式格式解下列初值问题:
![]()
取![]() 计算
计算![]() 并与准确解
并与准确解![]() 相比较。
相比较。
 视频学习资源下载
视频学习资源下载
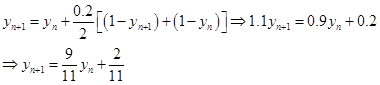 ,
, 