7.5 算法的稳定性及收敛性

7.5.1 稳定性

稳定性在微分方程的数值解法中是一个极其重要的问题。因为微分方程的数值解法是通过离散化将微分方程转化为差分方程（代数方程）来求解的，而在差分方程的求解过程中，存在着各种计算误差，这些计算误差如舍入误差等引起的扰动，在误差传播过程中，可能会大量积累，以至于“淹没”了差分方程的真解，例如，初值问题

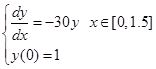
的精确解为

如分别用欧拉方法、经典R-K方法以及阿达姆斯四阶预测—校正方法分解，步长取为，算得的列于表7-7中。

表7-7

 

欧拉方法	经典R—K方法	阿达姆斯 预测—校正方法	精确解
-3.27675×104	1.18719×102	2.41152×106	2.86252×10-20

 

从表7-7可见，三种数值解法所得的结果相差悬殊，都与精确解相差至巨，这就是一个算法稳定性很差的例子。

当在某节点上的值有大小为δ的扰动时，如果在其以后的各节点上的值产生的偏差都不大于δ，则称这种方法是稳定的。

这里简单的以模型方程（或称为试验方程）

   　　　　　　　　　　　　　　　　　　　（7.5.1）

为例，对欧拉方法做稳定性分析。

先分析显式欧拉格式，对于式（7.5.1），有

将上式反复递推后，可得

或 

式中

要使有界，其充要条件为

即　　　

由于，故有

                    　　　　　　　　 （7.5.2）

可见，如欲保证算法的稳定，显示欧拉格式的步长的选取就要受到式（7.5.2）的限制。的绝对值越大，则限制的值就越小。

例如，初值问题

的精确解为

如取步长，作显式欧拉格式计算时，有

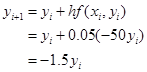
按上式计算所得结果列于表7-8中。

 

表 7-8

			精确解
	显式欧拉格式	隐式欧拉格式
0.05	-0.75000	1.42857╳	4.10425╳
0.10	1.12500	4.08163╳	3.36897╳
0.15	-1.68750	1.16618╳	2.76542╳
0.20	2.53125	3.33195╳	2.2699╳
0.25	-3.79688	9.51984╳	1.863╳
0.90	7.38946╳	8.04906╳	1.43126╳
0.95	-1.10842╳	2.29973╳	1.17485╳
1	1.66263╳	6.57066╳	9.64375╳

 

从表中的数值显示可见，这时的显式欧拉方法是不稳定的。究其原因，就是由于不符合式（7.5.2）的规定:

再分析隐式欧拉格式，对于式（7.5.1），有

所以   

由于,则恒有

故恒有　

因此隐式欧拉格式是绝对稳定（无条件稳定）的（对任何）。

对于初值问题

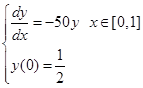
同样取步长，作隐式欧拉格式计算时，有

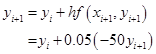
所以

按上式计算所得结果也列于表7-8中。从表中的数值可见，同样的步长，隐式欧拉方法却是稳定的。因为这时它对任何都是绝对稳定的。

稳定区域的定义：能保证该算法稳定的的取值范围，称为稳定区域，其中

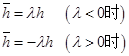
显然，稳定区域越大，意味着该算法的稳定性越好。

由式（7.5.2）可知，显式欧拉方法的稳定区域为

又由式（7.5.3）可知，隐式欧拉方法的稳定区域为

可见隐式欧拉方法的稳定性比显式欧拉方法的好。

可用与上述类似的方法来分析步阿达姆斯显式和隐式方法的稳定性。对于典型方程，它们的稳定区域如分别记为和,其数值如表7-9所示。

表 7-9

 

由表7-9可见：

（1） 阿达姆斯隐式方法的稳定区域都比同阶的显示方法的大，只是隐式方法最大的优点；

（2） 越大（即步数、阶数越大）时稳定区域就越小，只有隐式欧拉方法才是绝对稳定的。

5.2 收敛性

微分方程在离散为差分方程来求解，当步长时，存在着差分方程的解能否收敛到微分方程的准确解的问题。对于任意节点，当（同时）时，都能趋向于准确解的算法，称为是收敛的，否则称为不收敛。

这里简单的以欧拉方法为例，来分析其收敛性。

在欧拉格式

　　　　　　　　　　　　　　　　　（7.5.4）

中，如取，所得为

　　　　　　　　　　　　　　（7.5.5）

由式（7.2.3）可知，其局部截断误差为

必定存在常数，使

　　　　　　　　　　　　　　　　　（7.5.6）

局部截断误差的积累误差称为整体截断误差。下面我们来讨论整体截断误差。记

其中，为式（7.1.1）的精确值，为欧拉公式得到的近似解。

式（7.5.4）-式（7.5.5），有

　　　　　（7.5.7）

式中，是关于的李普西兹（Lipschitz）常数。因

将式（7.5.7）和（7.5.6）代入上式，可得

将上式反复递推后，可得

或

        　　（7.5.8）

设（为常数）

因为

所以

把上式代入式(7.5.8)，得

如不计初值误差，即，则有

                （7.5.9）

式（7.5.9）说明，当时，，即，因此欧拉方法是收敛的，且其收敛速度为，即具有一阶收敛速度。式（7.5.9）还说明欧拉方法的整体截断误差为，即是一阶的，因此算法的精度为一阶。

前面§2中的式（7.2.3）有

即欧拉方法的局部截断误差是二阶的，可见其整体截断误差（一阶）要比局部截断误差低一阶。这个结论对其它算法也适用，是带有普遍性的。