本章导入

在工程和科学技术的实际问题中，常需求解常微分方程。但常微分方程中往往只有少数较简单和典型的常微分方程（例如线性常系数常微分方程等）可求出其解析解。对于变系数常微分方程的解析求解就比较困难，而一般的非线性常微分方程就更不用说了。在大多数情况下，常微分方程只能用近似法求解。这种近似解法可分为两大类：一类是近似解析法，如级数解法、逐次逼近法等；另一类则是数值解法，它给出方程在一些离散点上的近似解。

在具体求解微分方程时，需要具备某种定解条件，微分方程和定解条件合在一起组成定解问题。定解条件有两种：一种是给出积分曲线在初始点的状态，称为初始条件，相应的定解问题称为初值问题；另一种是给出积分曲线首尾两端的状态，称为边界条件，相应的定解问题则称为边值问题。

学习目标

（1）了解常微分方程初值问题解法的一些基本概念。

（2）掌握一阶常微分方程初值问题的一些常用的数值计算方法如：欧拉方法，改进的欧拉方法，龙格—库塔方法，阿达姆斯方法。

（3）数值方法的收敛性和稳定性的概念。

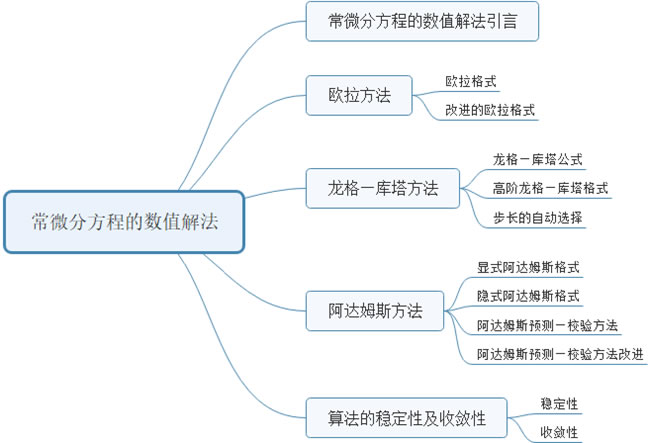
知识结构