1.第五公设问题

欧几里得《几何原本》中第一卷中所提第五公设：（在同一平面内）如果两条直线与第三条直线相交，某一侧的两个内角和小于二直角。则把两条直线向该侧充分6延长后一定相交

这条公设是欧氏几何学最早的平等公理，后来才改用现在惯用的普雷菲尔命题，这两个命题是等价的。人们经历了2000多年的时间，直到非欧几何的产生才真正认识到它在欧氏几何公理系统中的独立性和特殊地位。

从《几何原本》问世到19世纪30年代，在2000多年的漫长岁月中，许多数学家均试用《几何原本》中除第五公设以外的其它公设和它们的一切推论（即用绝对公理系统及其推论）来证明第五公设是一条定理。他们这样做的起因是：第一，第五公设不像前四条公设那样内容简单、直观，第二，它在《几何原本》中出现的较晚，只有在证明第29个命题时才第一次使用。

仔细分析这些数学家的证法，发现其错误之处多数是把与第五公设等价的命题作为论据，这些都不是第五公设外其余公设的推论，故所有这些论证都失败了。

下面罗列一些与第五公设等价的命题：

1）通过直线外一点只能引唯一一直线与它平行

2）两条平行线被第三条直线所截，同位角相等

3）在已知直线同侧与它有同样距离的点组成一直线

4）从两平行线中一条上的点到另一线的距离都相等

5）三角形的内角和等于两直角

6）相似三角形存在

7）一直线的垂线和斜线总相交

8）平面上存在一个内角和为的三角形

例如希腊人Proclus（公元前410-475年）对欧氏第五公设的证明

已知：如图所示，直线与直线、分别交于、两点，在直线的一侧构成内角（为直角）  

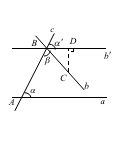
求证：、在这一侧相交

证明：过点引直线，且它与构成的与

角处于同位角的角满足。

于是.

在上取点，且在的内角和的一侧。

过作的垂线，垂足为，

则沿射线方向远离时，它到的距

离不断增大，且可取任何正数。

设平行线与的距离为，在上必存

在点，使，这必在上，

于是、在这一侧相交。

这个证明是无效的，其错误在于使用命题：“如果直线与平行，则它们之间的距离处处相等，这一事实的成立没有欧氏平行公理V是证明不了的，而平行公理与第五公设是等价的。

   2.非欧几何

在论证第五公设的过程中，著名数学家萨开里、勒让德等人，都试图用反证法来证明第五公设，他们从第五公设或其它等价命题的否定命题出发，经过严格地逻辑推理，得出许多和一系列命题，试图从中找到与绝对几何命题相矛盾的结果。然而他们并没有从中得出什么矛盾的结果，实际上这一系列新的命题就是非欧几何的内容。

①罗氏几何

罗巴切夫斯基试图用反证法证明第五公设，他保留了欧氏几何中除平行公理外的其它公理，并做假设命题“同一直线的垂线和斜线不一定相交，在此基础上展开了庞大而严密的罗加推导，得出许多命题，最终形成了没有矛盾的（即相容的）的新体系

②黎曼几何

黎曼几何是假设过直线外一点“不存在直线”与已知直线不相交这一命题成立，在此基础上展开的严密的逻辑推选导，最终形成的没有矛盾的几何新体系

 ③罗氏几何与黎曼几何的模型

 罗氏几何的（Cayley-F.kLein）模型

 在欧氏平面上任取一个圆，把圆内部的点所构成的集合看成是罗氏“平面”

 罗氏平面几何的原始概念解释成：

罗氏点：圆内的点

罗氏直线：圆内的开弦（两个端点除外，它们可称为无穷远点）

结合关系：圆内原来的点和统的结合关系

介于关系：圆内弦上三点的介于关系

运动关系：欧氏平面上，将圆K变成自身的射开方变换。

 罗氏平行公理（在罗氏平面上） 通过干线外一点至少存在两直线与已知直线不相交

黎曼几何的（F.KLein）模型

黎曼几何的原始概念解释成

黎氏点：欧氏球面上的点，但把每对对径点看成一点

黎氏直线：球面上的在圆

黎氏平面：改造后的球面

黎氏点与黎氏直线的基本关系

①通过任意两个黎氏点存在一条黎氏直线。

②通过任意两个黎氏点至多存在一条黎氏直线

③每条黎氏直线上至少有两个格外氏点；至少存在三个黎氏点不在同一条黎氏直线上

黎曼几何平行公理：黎氏平面上任意两条直线相交。