一、二次曲线的特征方程

已知二次曲线的一般方程

                 eq \o\ac(○,1)1

其 中不同时为零，经过旋转坐标轴消去 项，方程 eq \o\ac(○,1)1化为

                eq \o\ac(○,2)2

不变式

     

根据一元二次方程的根与系数的关系，即韦达定理，不难看出 和 正好是方程

                eq \o\ac(○,3)3

的两个根。

方程 eq \o\ac(○,3)3称为二次曲线 eq \o\ac(○,1)1的特征方程，其根记作 ，称为 eq \o\ac(○,1)1特征根。

由于 是正交变换下的不变量，所以特征方程及其特征根都是正交变换下的不变量

 

二、利用不变量化简方程

仅就常态二次曲线 给出化简方法。

（1）设 方程 eq \o\ac(○,2)2经过坐标轴的平移变为

                     eq \o\ac(○,4)4

这时

 

所以

又因为 为特征方程 eq \o\ac(○,3)3的两个根 和 ，因此方程 eq \o\ac(○,4)4可改写成

（或 ） eq \o\ac(○,5)5

 eq \o\ac(○,5)5中各项系数都是不变量，可通过方程 eq \o\ac(○,1)1的系数求出。从而是方程 eq \o\ac(○,1)1化简的标准方程。

在 时，方程 eq \o\ac(○,5)5可能是椭圆或双曲线。这从特征根 和 的关系中可区分出来。

下面判断 和 究竟哪一个是 ，哪一个是 。

在§2.8推导坐标变换不变量时，已得出 ，

两边都乘上 得：

。

于是当 时，有 即 ；

当 时，有 即 。

就是说当 时，取 为 和 中最大者；

当 时，取 为 和 中最小者。

当 时，方程 eq \o\ac(○,1)1就是方程 eq \o\ac(○,2)2，系数 就是 ，若 时， 取 和 中最大者，若 ， 取 和 最小者。

（2）设 ，有 ， 和 必有一个为零，究竟谁为零与 有关。

据前面已推出的条件 ，

1）当 时，有 即

又

不妨设 ，于是， ，根据 ，

必有 ，经坐标平移，方程 eq \o\ac(○,2)2可化成

                    eq \o\ac(○,6)6

不变量形式有

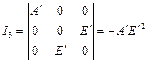
方程 eq \o\ac(○,6)6可改写成

                eq \o\ac(○,7)7

2）当 时，有 即

又

不妨设 ，于是， ，根据 ，

必有 ，经坐标平移，方程 eq \o\ac(○,2)2可化成

                    eq \o\ac(○,8)8

不变量形式有

 

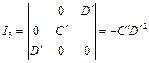
方程 eq \o\ac(○,8)8可改写成       

                     eq \o\ac(○,9)9

例  判断下列曲线的类型，并化成标准式。

（1）

（2）

（3）

（1）解：

1）求不变量

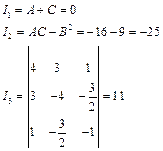
2）由于 且 ，故曲线为双曲线。

3）化简方程为标准形式：

特征方程为 ，

故特征根为 ，

又因为 ，故取 ，

而 ，

方程化为： ，或 。

 

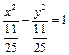（2）解：

1）求不变量

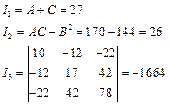
2）由于 且 ，故曲线为椭圆。

3）特征方程为 ，

故特征根为 ，

又因为 ，故取 ，

而

方程化为

（3）解：

1）求不变量

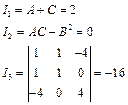
2）判别类型，

由于 且 ，故曲线为抛物线。

3）化方程为标准形式，

因为 ，方程可简化为

即 .

 

方程
判别式	类型	一般情形	特殊情形
	椭圆型	椭圆或圆	一点或没有轨迹
	双曲型	双曲线	两条相交直线
	抛物线型	抛物线	两条相交直线；两条重合直线或没有轨迹

 

方程
类型		标准方程	特征方程
椭圆型		（ 为特征根）
双曲型		（ 为特征根）
抛物线型		或