一．填空题（每小题4分，共20分）

1.已知向量 ，则 与 的夹角为       。

2.在正交变换下矩形变成               。

3.设有共线三点，则单比                   。

4.如果公理系统的所有模型都是同构的，则称它是         的公理系统。

5.无穷远直线所对应的齐次方程是             。

二．选择题（每小题4分，共20分）

1.设三个向量 满足 ，则 =（        )。

A．       B．      

C．      D．  

2. 设点共线，且在仿射变换下分别变成，则三点（        ）。

A．共线              B．三角形顶点      

C．可能不共线        D．可能重合

3. 正方形的下列性质中哪些是仿射的(         )。

(1)对边平行；            (2)四角相等；

(3)四边相等；            (4)对角线互相平分；

(5)对角线互相垂直；      (6)角被对角线平分；

(7)对角线相等；          (8)面积

A．(1)，(4)                  B．(5)，(6)      

C．(1)，(3)，(4)，(6)        D．(2)，(3)，(7)，(8)

4.三角形内一点在仿射变换下变成（         ）。

A．三角形外一点          B．三角形的顶点      

C．三角形内一点           D．三角形边上的内点

5.下列曲线中是椭圆型的是（          )。

A． 

B．

C．  

D．

三．简答题（共10分）

试着陈述非欧几何是怎样产生的？

四、计算与证明题（共50分）

1.（15分） 求将点分别变成的正交变换公式。

2.（10分）证明直线将两点与的连线段分成的比是。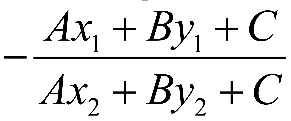

3.（10分）若存在，求下列各点的非齐次坐标：

，。

4．（15分）判断二次曲线的类型,求其简化方程及相应的坐标变换公式。