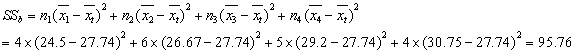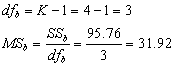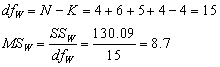当前位置 > 第七章 方差分析 > 第二节 单因素方差分析
七、应用实例
【例7.1】调查四个行业某一时期的利润情况，结果如下图所示。按图统计结果，计算四个行业的平均利润是否有差异。
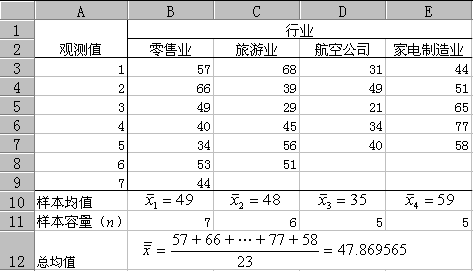
图7-1 四个行业的利润统计图
【解】SST = (57-47.869565)2+…+(58-47.869565)2=115.9295
SSA = 1456.608696
SSE = 2708
?
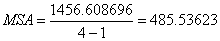
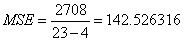
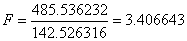从F值可以看出，大于临界值（3.12），所以，拒绝原假设，认为四个行业至少有两个行业的利润率有显著差异。
【例7.2】从某学校同一年级中随机抽取19名学生，再将他们随机分成4组，在2周内4组学生都用120分钟复习同一组英语单词。
表7-2 4组学生英语单词测验成绩情况
| 序号 |
第一组A |
第二组B |
第三组C |
第四组D |
1 |
24 |
29 |
30 |
27 |
2 |
26 |
25 |
28 |
31 |
3 |
20 |
21 |
32 |
32 |
4 |
28 |
27 |
30 |
33 |
5 |
|
28 |
26 |
|
6 |
|
30 |
|
|
N |
4 |
6 |
5 |
4 |
均值 |
24.5 |
26.67 |
29.2 |
30.75 |
标准差 |
3.42 |
3.27 |
2.28 |
2.63 |
第一组每个星期一一次复习60分钟；第二组每个星期一和三两次各复习30分钟；第三组每个星期二、四、六三次复习各20分钟；第四组每天（星期天除外）复习10分钟。2周复习之后，相隔2个月再进行统一测验，其结果如下表所示。运用方差分析法可以推断分析的问题是：这4种复习方法的效果之间有没有显著性差异？
【解】1.确定类型：由于19名学生是以随机方式被分配到四个实验组的，所以这四组样本是四个独立样本。
2.用方差分析方法对四组总体平均数差异进行综合性地F检验
检验步骤如下：
第一步，提出假设：
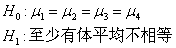
第二步，因为是四个独立样本，所以选择：
???用上述公式来计算F检验统计量的值。由第四章第三节中加权平均数的计算公式得到：
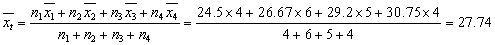
则：
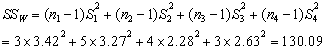
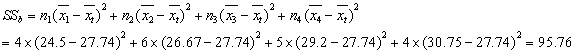
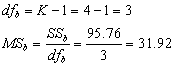
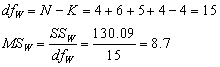
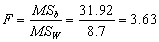
第三步，统计决断：
根据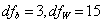
，α=0.05，查F值表，得到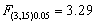 
由于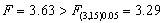
，即P（ F > 3.08）< 0.05 ,所以拒绝零假设，接受备择假设，即至少有两种复习方法有显著性差异。