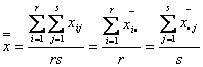当前位置 > 第七章 方差分析 > 第三节 双因素方差分析

第三节　双因素方差分析

　　一、双因素方差分析的类型
　　如果方差分析只针对一个因素进行，称为单因素方差分析，如果同时针对两个因素进行则称为双因素分析(two-way analysis of variance)。如前面讲的例子，我们除了关心饮料颜色对销售量的影响之外，还想了解销售地区对销售量的影响，即同时分析饮颜色（因素A）和销售地区（因素B）这两个因素对销售量的影响。就属于双因素方差分析。双因素方差分析的内容，是对两个影响因素进行检验，分析究竟一个因素在起作用，还是两个因素都起作用，或是两个因素的影响都不显著。
　　双因素方差分析有两种类型：一种是无交互作用的双因素方差分析，它假定因素A和因素B的效应之间是相互独立的，不存在相互关系；另一种是有交互作用的方差分析，它假定A、B两个因素不是独立的，而是相互起作用的，两个因素同时起作用的结果不是两个因素分别作用的简单相加，两者的结合会产生一个新的效应。这种效应的最典型的例子是，耕地深度和施肥量都会影响产量，但同时深耕和适当的施肥可能使产量成倍增加，这时，耕地深度和施肥量就存在交互作用。两个因素结合后就会产生出一个新的效应，属于有交互作用的方差分析问题。本文主要论述无交互作用的双因素方差分析。

　　 二、数据结构
　　（一）双因素方差分析的假定条件
　　1.个总体都服从正态分布：对于因素的每一个水平，其观察值是来自正态分布总体的简单随机样本；
　　2.各个总体的方差必须相同：对于各组观察数据，是从具有相同方差的总体中抽取的；
　　3.观察值是独立的
　　（二）数据结构
　　表7-3　互作用双因素方差分析的数据结构

　　设两个因素分别是A和B。因素A共有r个水平，因素B共有s个水平，无交互作用的双因素方差分析的数据结构如表7-3所示。
　　（三）分析步骤
　　1.模型与建立假设
　　方差分析模型如下：
　　
　　其中Xij表示第i组的第j个观察值；μ表示总体的平均水平；aj表示影响因素A在i水平下对应变量的附加效应，bj表示影响因素B在j水平下对应变量的附加效应，并满足：
　　
　　
　　eij为一个服从正态分布的随机变量，代表随机误差。我们检验因素A是否起作用实际上就是检验各个aj是否均为0，如都为0，则因素A所对应的各组总体均数都相等，即因素A的作用不显著；对因素B，也是这样。因此原假设有两个：
　　对因素A：
　　对因素B：
　　2.构造检验F统计量
　　（1）水平的均值
　　
　　
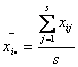
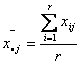
　　（2）总均值
　　

下一页