双因素方差分析同样要对总离差平方和SST进行分解,SST分解为三部分:SSA、SSB和SSE,以分别反映因素A的组间差异、因素B的组间差异和随机误差的离散状况。
它们的计算公式分别为:
SSE = SST—SSA—SSB
(4)构造检验统计量
由平方和与自由度可以计算出均方,从而计算出F检验值,如表7-4。
表7-4 无交互作用的双方差分析表
当前位置 > 第七章 方差分析 > 第三节 双因素方差分析
(3)离差平方和的分解
双因素方差分析同样要对总离差平方和SST进行分解,SST分解为三部分:SSA、SSB和SSE,以分别反映因素A的组间差异、因素B的组间差异和随机误差的离散状况。
它们的计算公式分别为:
![]()
![]()
![]()
SSE = SST—SSA—SSB
(4)构造检验统计量
由平方和与自由度可以计算出均方,从而计算出F检验值,如表7-4。
表7-4 无交互作用的双方差分析表
方差来源 |
离差平方和 |
df |
均方MS |
F |
因素A |
SSA |
r-1 |
MSA = SSA /(r-1) |
MSA/MSE |
因素B |
SSB |
s-1 |
MSB = SSE /(n-r) |
MSB/MSE |
误差 |
SSE |
(r-1)(s-1) |
MSE= SSE /(r-1)(s-1) |
— |
总方差 |
SST |
n-1 |
— |
— |
为检验因素A的影响是否显著,采用下面的统计量:
![]()
为检验因素B的影响是否显著,采用下面的统计量:
![]()
3.判断与结论
根据给定的显著性水平α在F分布表中查找相应的临界值Fa,将统计量F与Fa进行比较,作出拒绝或不能拒绝原假设H0的决策。
若A统计量大于临界值,则拒绝原假设1,表明均值之间有显著差异,即因素A对观察值有显著影响;若A统计量小于临界值,则不能拒绝原假设1,表明均值之间的差异不显著,即因素A对观察值没有显著影响;同理,若B的统计量大于临界值,则拒绝原假设2,表明均值之间有显著差异,即因素B对观察值有显著影响。 若B统计量小于临界值,则不能拒绝原假设2,表明均值之间的差异不显著,即因素B对观察值没有显著影响。
(三)实例
【例7.3】有四个品牌的彩电在五个地区销售,为分析彩电的品牌(品牌因素)和销售地区(地区因素)对销售量是否有影响,对每个品牌在各地区的销售量取得以下数据。试分析品牌和销售地区对彩电的销售量是否有显著影响?(a=0.05)
表7-5 不同品牌的彩电在各地区的销售量数据
| 品牌因素 |
地区因素 |
||||
地区1 |
地区2 |
地区3 |
地区4 |
地区5 |
|
品牌1 |
365 |
350 |
343 |
340 |
323 |
【解】我们可以按上述的步骤,完成检验,但计算工作量很大。这里我们利用Excel的分析工具。
首先针对问题,作原假设和备择假设:
对因素A:![]() ;
;![]() 不全等
不全等
对因素B:![]() ;
;![]() 不全等
不全等
 Excel解决方案 |
①将数据输入工作表中 |
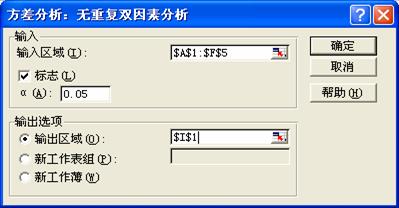
图7-1 “方差分析:无重复双因素方差分析”分析工具对话框
利用excel,得到的方差分析表见表7-6。
表7-6 无重复双因素方差分析结果
| 差异源 |
SS |
df |
MS |
F |
P-value |
F crit |
行(品牌) |
13004.55 |
3 |
4334.85 |
18.10777 |
9.46E-05 |
3.4903 |
列(地区) |
2011.7 |
4 |
502.925 |
2.100846 |
0.143665 |
3.2592 |
误差 |
2872.7 |
12 |
239.3917 |
- |
- |
- |
总和 |
17888.95 |
19 |
- |
- |
- |
- |
结论:∵FA=18.10777>Fa=3.4903≥Fa=3.4903
∴拒绝原假设1,说明彩电的品牌对销售量有显著影响;
∵FA=2.100846< Fa=3.2592< Fa
∴不能拒绝原假设2,不能认为销售地区对彩电的销售量有显著影响。