与一元线性回归分析相比，多元回归分析涉及的自变量更多，回归模型和方程式更复杂，计算量更大，但是两者所采用的回归分析原理和方法是相似的。
一、多元线性回归方程
多元线性回归方程是表达一个因变量与2个或2个以上的自变量之间的线性依存关系的一种多元线性回归模型的估计式。
多元线性回归模型的一般表达式为：
上式中，b0表示截距，bi分别表示与
个自变量想联系的斜率(或称为偏回归系数)，ui表示剩余残差项或称为随机扰动项，假定
。 多元线性回归方程为：
上式中，
表示多元线性回归模型的估计式，当回归系数都确定后，代如各自变量的值后得到的是多元线性回归模型的估计值。式中bi的含义与式(8.1)中的相同。各自变量xij的下标
、
、……、
，其中1，2，……
代表第
个自变量，
代表某个自变量的样本数据的顺序号，
=1，2，……，n。对自变量下标的解释同样适用式(8-1)。式(8.2)中的参数可由最小平方法导出的正规方程组解出，即(为简便起见，数据的顺序号
省略)： 
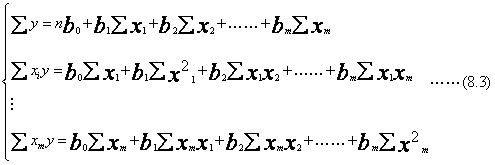
当自变量超过三个时，一般要用矩阵形式通过计算机调用多元回归分析的软件包来求出回归参数。下面以二元线性回归模型和相应的估计式——二元线性回归方程作为多元线性回归分析的特例来加以介绍。
二个自变量分别与一个因变量Y之间呈线性相关时，可用二元线性回归模型来表示：
上式中，ui表示剩余残差项或称为随机扰动项，
。 上式的估计式，即二元线性回归方程为：
在上式中，ui表示二元线性回归的估计值；与式(8.4)中的b0相同，b0表示Y平面的截距，即当两个x都为0时Y的均值；b1和b2的解释与式(8-4)中的也相同。b1表示x2保持不变，x1增加一个单位时
的平均变动量；b2表示x1保持不变x2增加一个单位时Y的平均变动量；故b1和b2分别表示与自变量x1和x2相联系的斜率，又称之0为偏回归系数。 为确定b0、b1、b2设：
分别对
求偏导数并令其为零，即令： 
得到下面的正规方程组：
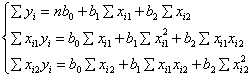
通过解这个正规方程组得到二元线性回归方程中的b0、b1和b2。
二、元线性回归方程的效果检验
(一)回归方程的显著性检验
用以判定回归的效果是否显著，即所拟和的回归方程用来解释因变量的变动是否有效，常用的方法之一是作F检验。多元线性回归方程效果检验的具体步骤为：
1.计算剩余离差平方和SE
2.计算回归离差平方和SR
3.计算检验统计量F的值
其中：n——样本容量(即观察数据个数)；
m——自变量的个数。
4.查F检验临界值表判别显著性
根据给定的已知条件之一，即显著水平
，查F检验临界值表得到临界值
。若检验统计量F>Fa，则认为回归效果显著；若检验统计量F<Fa,则认为回归效果不显著。