用以检验回归方程中的参数(或系数)作用是否显著，可用t检验法。
在多元回归分析中，如果某个自变量xi对因变量y的作用不显著，则这个自变量前的回归系数bj就可视为0。但需要指出的是：回归系数与0的差异是否大，不能根据回归系数的绝对值大小来判断，而要根据统计假设检验的理论为依据。在前面作一元回归时，对回归方程做检验时，没有介绍回归系数的t 检验。这是因为在一元回归分析中，相关系数检验、方差分析中的F检验和回归系数的t检验是具有同等作用的。只要检验其中之一就可以达到对回归方程的显著性检验的目的。但是在多元回归分析中，对多元回归方程中各个自变量相联系的回归系数应逐一进行统计检验，不能用前述的两种检验来取代。
对回归系数作t检验的步骤可归纳为：
1.计算回归估计标准误差Syx
在多元线性回归分析中，回归估计标准误差Syx的计算公式为：
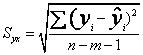
上式的根式中的分子项是实际值与估计值之差的平方和，即称之为剩余离差平方和SE；其分母项是自由度，即样本数据数减去自变量个数m后再减1，此式中的自由度计算方法和一元线性回归分析中的Syx相一致，在一元线性回归中，自变量个数m=1，则自由度为(n-1-1)=n-2。
2.计算
。 Cij是下列矩阵
的逆矩阵L-1中j行j列元素(即逆矩阵L-1主对角线上的j个元素)。 
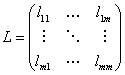
这里
上式中：
为第i个自变量的第t个样本数据； 
为第i个自变量样本数据的平均数，
为第j个自变量样本数据的平均数，
3.计算检验统计量tj
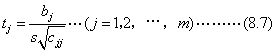
式中bj——第j个自变量前的偏回归系数；
S——回归估计标准误差Syx
4.查表检验显著性。
按显著性水平
查自由度为n-m-1的t检验临界值表(双侧)得到临界值 
若检验统计量
>
，认为回归系数与0有显著差异，相应的自变量就保留在多元回归方程中；若
<
，就认为该回归系数与0无显著差异，此时与相应的自变量就从多元回归方程中剔除，使建立的多元回归方程更符合实际情况。在一些情况下，如果在建立一个多元线性回归方程的过程中，同时有几个回归系数不能通过t检验，一般应剔除其中检验统计量t值最小所对应自变量后，重新建立更加简单的回归方程，然后再逐个进行回归系数的检验，反复进行到所有的回归系数都与0有显著差异时为止。