附录一：数据处理

1. 粒子动能的能量损失修正

粒子与物质相互作用是一个很复杂的问题，如何对其损失的能量进行必要的修正十分重要。

①粒子在Al膜中的能量损失修正

在计算粒子动能时还需要对粒子穿过Al膜（220：200为NaI（TI）晶体的铝膜密封层厚度，20为反射层的铝膜厚度）时的动能予以修正，计算方法如下：

设粒子在Al膜中穿越x的动能损失为E，则：

                                           （2.4.10）

其中（<0)是Al对粒子的能量吸收系数，（是Al的密度），是关于E的函数，不同E情况下的取值可以通过计算得到。可设=K（E），则E= K（E）x；取x→0，则粒子穿过整个Al膜的能量损失为：

                                          （2.4.11）

即                                        （2.4.12）

其中d为薄膜的厚度，为出射后的动能，为入射前的动能。由于实验探测到的是经Al膜衰减后的动能，所以经式（2.4.12）可计算出修正后的动能（即入射前的动能）。表1列出了根据本计算程序求出的入射动能和出射动能的对应关系：                           

 

 

 

 

 

 

 

 

表     1

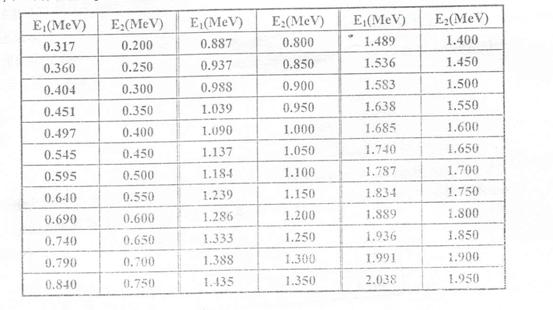
实验中可由测得的值，根据上表，用线性插值求得

②粒子在有机塑料薄膜中的能量损失修正

此外，实验表明封装真空室的有机塑料薄膜对存在一定的能量吸收，尤其对小于0.4MeV的粒子吸收近0.02MeV。由于塑料薄膜的厚度及物质组分难以测量，可采用实验的方法进行修正。实验测量了不同能量下入射动能和出射动能（单位均为MeV）的关系，采用分段插值的方法进行计算。具体数据如下：

2. 数据处理的计算方法和步骤（举例说明）：

设对探测器进行能量定标（操作步骤中的第5、6步）的数据如下：

实验测得当探测器位于25cm时的单能电子峰道数为220，求该点所得粒子的动能、动量及误差，已知源位置坐标为10cm、平均磁场强度为642.8高斯（Gs）。

    ①根据能量定标数据求定标曲线

已知：E1=0.661MeV，CH1=158.8；E2=1.17MeV，CH2=283.2；E3=1.33MeV，CH3=321.0；根据最小二原理用线性拟合的方法求能量E和道数CH之间的关系：

         

可以推导，其中：

       

             

              

带入上述公式计算可得：

     ②求粒子动能

     对于X=25cm处的粒子：

     1）将其道数220代入求得的定标曲线，得动能E2=0.9108MeV，注意；此为粒子穿过总计220厚铝膜后的出射动能，需要进行能量修正；

     2）在前面所给出的穿过铝膜前后的入射动能E1和出射动能E2之间的对应关系数据表中取E2=0.9108MeV前后两点作线性插值，求出对应于出射动能E2=0.9108MeV的入射动能E1=0.9990MeV

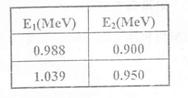
     3）上一步求得的E1为粒子穿过封装真空室的有机塑料薄膜后的出射动能E0，需要再次进行能量修正求出之前的入射动能EK，同上面一步，取E0=0.9990 MeV前后两点作线性插值，求出对应于出射动能E0=0.9990 MeV的入射动能EK=1.006MeV；

                            

     ③根据粒子动能由动能和动量的相对论关系求出动量PC（为与动能量纲统一，故把动量P乘以光速，这样两者单位均为MeV）的理论值

     由得出：

 

 

首页 上一页 下一页