第二单元 原子核物理
基础知识
一、核物理实验概述
随着原子核物理研究的深入,加深了人们对微观世界的认识,也推动了如核能利用,核辐射在工农业和医疗中的利用等等有关原子核的现代科学技术的发展。核物理实验是研究核反应、核应用的重要手段。随着人们在核实验中对和核辐射了解的深入,核实验技术也正成为许多其它学科诸如固体物理、天体物理、考古学等的重要研究手段。
核物理实验探测的对象主要是核衰变时所辐射的![]() 、
、![]() 射线和中子。因为这些粒子的尺度非常小,用最先进的电子显微镜也不能观察到,只能根据它们与物质相互作用产生的各种效应实现探测之目的,现已制造了多种类型的射线探测器。
射线和中子。因为这些粒子的尺度非常小,用最先进的电子显微镜也不能观察到,只能根据它们与物质相互作用产生的各种效应实现探测之目的,现已制造了多种类型的射线探测器。
探测器大致可分为“径迹型”与“信号型”两大类。“径迹型”探测器能给出粒子运动的径迹,如核乳胶、固体径迹探测器、威尔逊云室、气泡室、火花室等。这些探测器大多用于高能物理实验。“信号型”探测器则当一个辐射粒子到达时给出一个信号。根据工作原理的不同又可以分成气体计数器、闪烁计数器和半导体(固体)探测器三种,这是我们在低能核物理实验中最常用的探测器。
在核物理实验中测量的主要是辐射粒子的强度(单位时间内接收粒子的数目)、能谱(强度随能量的分布)、角分布(强度随角度的分布)以及它们随时间的变化关系。对于探测器和有关核电子学仪器装置的基本要求,就是把入射粒子的强度、它的能量大小和粒子到达的时间记录下来。核辐射粒子进入探测器产生一个信号(输出脉冲),信号幅度与辐射粒子能量之间的比例关系以及探测器的效率、能量分辨率和输出脉冲的波形是我们选择探测器时要考虑的重要因素。
探测器的效率定义为探测器中产生的可被检测的信号计数与入射粒子数的比值。探测效率不仅与粒子的性质有关,也与粒子的能量有关。对于低能辐射,若所产生的信号幅度比噪声小则将无法检测。入射粒子可被检测时所需要在探测器中损耗的最低能量称为该探测器的灵敏度。影响探测效率的另一因素是分析信号所用的电子学设备尚存在对灵敏度的限制。
探测器的能量分辨率是指探测器对于能量很接近的辐射粒子加以区别的能力。能量分辨率取决于相同能量的辐射所产生的脉冲幅度分布的展宽程度。图2.0-1表示一种典型的脉冲幅度分布。以百分比表示的能量分辨率![]() 的定义如下:
的定义如下:
![]()
![]() 越小,分辨能力越强。
越小,分辨能力越强。
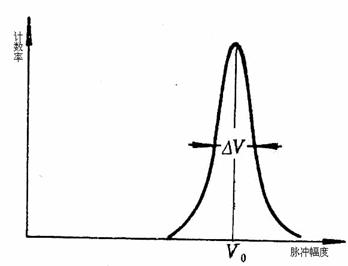
图2.0-1探测器的能量分辨率
在核物理的研究中一些重要的实验方法如下:
1. 散射实验 卢瑟福利用原子对![]() 粒子的散射确定了原子的核模型。康普顿(
粒子的散射确定了原子的核模型。康普顿(![]() )的
)的![]() 射线散射实验(康普顿散射)证实了光子是具有能量
射线散射实验(康普顿散射)证实了光子是具有能量![]() 和动量p=
和动量p=![]() k的粒子,在微观的光子与电子的相互作用过程中,能量与动量守恒仍然成立。历史上的散射实验在研究核辐射粒子与物质的相互作用时发挥了重要的作用。
k的粒子,在微观的光子与电子的相互作用过程中,能量与动量守恒仍然成立。历史上的散射实验在研究核辐射粒子与物质的相互作用时发挥了重要的作用。
2. 符合测量技术 在核现象中,有许多时间上相互关联的事件,这种相关的事件往往反映了原子核内在的运动规律。例如核级联衰变时所放射的粒子之间在时间上是相关的,级联衰变的平均时间间隔就是核激发态的平均寿命;又如上述衰变的粒子还有方向上的相关性即方向角关联。通过这些相关现象的研究可了解原子核结构和转化的规律。符合测量就是研究相关事件的一种方法。近30年来由于快电子学、多道分析器和多参数分析系统(直接测定核反应过程中各种参数之间的相互关系)的发展和电子计算机在核物理实验领域中的应用,符合方法已成为实现多参数测量的必不可少的实验手段。
3.
能谱测量技术 测量带电粒子能量的方法最简单的是射程测量方法。这种方法比较粗糙已较少应用。第二种是能量灵敏探测器方法,它包括电离室、正比计数器、闪烁计数器和半导体探测器。利用探测器的输出脉冲幅度与入射粒子能量成正比这一规律,通过脉冲幅度与时间变换器把不同幅度的脉冲信号记录下来,再根据脉冲幅度确定粒子能量。第三种方法是能量色散的方法(又称磁分析法),如![]() 和
和![]() 磁谱仪等。它利用不同能量的粒子因其动量不同造成在磁场中运动的轨迹不同而把具有不同能量的粒子分开,目前它仍然是分辨率最好、精度最高的方法。
磁谱仪等。它利用不同能量的粒子因其动量不同造成在磁场中运动的轨迹不同而把具有不同能量的粒子分开,目前它仍然是分辨率最好、精度最高的方法。
4. 时间谱测量技术 测量核事件之间短的时间间隔如测量核激发态的短寿命、正电子在各种物质中的平均湮没寿命、核粒子的飞行时间等是核物理实验的一项重要技术。时间谱测量技术也是一种能谱测量技术,如中子谱、带电粒子的飞行时间(TOF)谱,近几年来时间测量技术得到越来越广泛的应用。
二、核衰变的统计规律和放射性测量的统计误差
我们知道核衰变的过程是相互独立、彼此无关的,每个原子核发生衰变的时间纯属偶然而无法确定,但是对于大量原子核![]() ,经过时间
,经过时间![]() 后,平均地说其数目将按指数规律
后,平均地说其数目将按指数规律![]() 衰减,
衰减,![]() 为衰变常数,它与放射源的半衰期
为衰变常数,它与放射源的半衰期![]() 之间满足公式:
之间满足公式:![]() 。
。
在![]() 时间内平均衰变的原子核的数目
时间内平均衰变的原子核的数目![]() 为
为
![]() (
(
根据上式,统计平均看,在![]() 个原子核中有
个原子核中有![]() 个核发生衰变的概率为
个核发生衰变的概率为
![]() (
(
上式中系数![]() 是考虑了
是考虑了![]() 个原子核中发生衰变的
个原子核中发生衰变的![]() 个核的各种可能的组合数。现设原子核总数
个核的各种可能的组合数。现设原子核总数![]() ,测量时间
,测量时间![]() 远小于放射源的半衰期
远小于放射源的半衰期![]() ,即
,即![]() ,也即衰变数
,也即衰变数![]() 远小于粒子总数
远小于粒子总数![]() 。这时式(
。这时式(![]() …,
…,![]() 均可用
均可用![]() 代替,于是有
代替,于是有
![]()
由式(![]() ,则有
,则有
![]() (
(
这就是泊松分布。它告诉我们如果在时间间隔![]() 内平均衰变次数为
内平均衰变次数为![]() ,则在时间间隔
,则在时间间隔![]() 内衰变数为
内衰变数为![]() 出现的概率
出现的概率![]() 即如式(
即如式(![]() 时的泊松分布图。
时的泊松分布图。
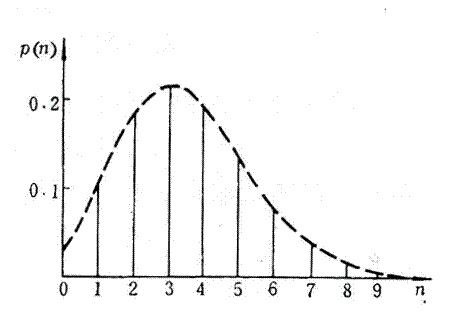
图2.0
泊松分布有下列四个重要性质:
1. 满足归一化条件
![]()
2. 根据式(![]() 时间内平均衰变数应为
时间内平均衰变数应为
![]()
3. 每次测量得到的衰变数![]() 与平均衰变数之间的偏差的平均值为0,即
与平均衰变数之间的偏差的平均值为0,即