

二、有序搜索
下面学习有序搜索
1.定义
用估价函数f来排列GRAPHSEARCH第8步中OPEN表上的节点。应用某个算法(例如等代价算法)选择OPEN表上具有最小f值的节点作为下一个要扩展的节点。这种搜索方法叫做有序搜索(ordered search)或最佳优先搜索(best-first search),而其算法就叫做有序搜索算法或最佳优先算法。
尼尔逊(Nilsson)曾提出一个有序搜索的基本算法。估价函数f是这样确定的:一个节点的希望程序越大,其f值就越小。被选为扩展的节点,是估价函数最小的节点。
2.实质
选择OPEN表上具有最小f值的节点作为下一个要扩展的节点,即总是选择最有希望的节点作为下一个要扩展的节点。
3.有序状态空间搜索算法
①把起始节点S放到OPEN表中,计算f(S)并把其值与节点S联系起来。
②如果OPEN是个空表,则失败退出,无解。
③从OPEN表中选择一个f值最小的节点i。结果有几个节点合格,当其中有一个为目标节点时,则选择此目标节点,否则就选择其中任一个节点作为节点i。
④把节点i从OPEN表中移出,并把它放入CLOSED的扩展节点表中。
⑤如果i是个目标节点,则成功退出,求得一个解。
⑥扩展节点i,生成其全部后继节点。对于i的每一个后继节点j:
a)计算f(j)。
b)如果j既不在OPEN表中,又不在CLOSED表中,则用估价函数f把它添入OPEN表。从j加一指向其父辈节点i的指针,以便一旦找到目标节点时记住一个解答路径。
c)如果j已在OPEN表上或CLOSED表上,则比较刚刚对j计算过的f值和前面计算过的该节点在表中的f值。如果新的f值较小,则
i 以此新值取代旧值。
ii 从j指向i,而不是指向它的父辈节点。
iii 如果节点j在CLOSED表中,则把它移回OPEN表。
⑦转向②,即GO TO②。

宽度优先搜索、等代价搜索和深度优先搜索与有序搜索之间有什么关系?
4.有序搜索方法分析
宽度优先搜索、等代价搜索和深度优先搜索统统是有序搜索技术的特例。对于宽度优先搜索,选择f(i)作为节点i的深度。对于等代价搜索,f(i)是从起始节点至节点i这段路径的代价。
有序搜索的有效性直接取决于f的选择,如果选择的f不合适,有序搜索就可能失去一个最好的解甚至全部的解。如果没有适用的准确的希望量度,那么f的选择将涉及两个方面的内容:一方面是一个时间和空间之间的折衷方案;另一方面是保证有一个最优的解或任意解。
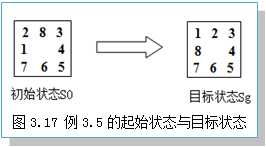
例3.5 八数码难题。
用有序搜索求解八数码问题,其起始状态和目标状态如图3.17所示。设估价函数:f(x)=d(x)+h(x),其中:d(x)表示节点x的深度,h(x)表示节点x的棋局与目标节点格局位置不相同的数码数目。
该问题的有序搜索树如图3.18所示,其中节点旁括号外的数字表示相应节点的生成顺序,括号内容的数字表示相应节点的启发式函数值,节点中红色的数码表示错放的数码,红色边表示解路径。

