您的当前位置是：第三章 确定性推理>>学习内容>>知识点四

一、博弈树概念

1．分钱币的游戏

有一堆数目为N的钱币，由两位选手轮流进行分堆，要求每个选手每次只把其中某一堆分成数目不等的两小堆。例如，选手甲把N分成两堆后，轮到选手乙就可以挑其中一堆来分，如此进行下去，直到有一位选手先无法把钱币再分成不相等的两堆时就得认输。

设初始状态为（7，MIN），由MIN先分，建立问题的状态空间图3.21，图中所有终结点均表示该选手必输的情况，取胜方的目标是设法使棋局发展为结束在对方走步时的终结点上。

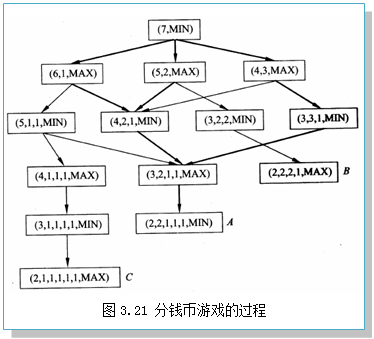
结点A是MAX的搜索目标，而结点B，C则为MIN的搜索目标。

搜索策略要考虑的问题是：

①对MIN走步后的每一个MAX结点，必须证明MAX对MIN可能走的每一个棋局对弈后能获胜，即MAX必须考虑应付MIN的所有招法，这是一个与的含意，因此含有MAX符号的结点可看成与结点。

②对MAX走步后的每一个MIN结点，只须证明MAX有一步能走赢就可以，即MAX只要考虑能走出一步棋使MIN无法招架就成，因此含有MIN符号的结点可看成或结点。

对弈过程的搜索图呈现出与或图表示的形式。实现一种取胜的策略就是搜索一个解图的问题，解图就代表一种完整的博弈策略。

2．二人零和、全信息、非偶然博弈定义

二人零和:对垒的A，B双方轮流采取行动，博弈的结果只有三种情况：A方胜，B方败；B方胜，A方败；双方战成平局。

全信息:在对垒过程中，任何一方都了解当前的格局及过去的历史。

非偶然:任何一方在采取行动前都要根据当前的实际情况，进行得失分析，选取对自己最为有利而对对方最为不利的对策，不存在“碰运气”的偶然因素。即双方都是很理智地决定自己的行动。

这类博弈的实例有：一字棋、余一棋、西洋跳棋、国际象棋、中国象棋、围棋等。对于带机遇性的任何博弈，因不具有完备信息，不属这里讨论范围，但有些论述可推广到某些机遇博弈中应用。

3．博弈树

在博弈过程中，任何一方都希望自己取得胜利。因此，当某一方当前有多个行动方案可供选择时，他总是挑选对自己最为有利而对对方最为不利的那个行动方案。这样，如果站在某一方（如A方，即在A要取胜的意义下），把上述博弈过程用图表示出来，则得到的是一棵“与或树”。

从MAX方的观点看，在博弈过程的每一步，可供自己选择的行动方案之间是“或”的关系，原因在于选择哪个方案完全是由自己决定的；而可供MIN选择的行动方案之间则是“与”的关系，原因是主动权掌握在MIN手里，任何一个方案都有可能被MIN选中，MAX必须防止那种对自己最为不利的情况的发生。

这样，从选手的角度看，博弈树就是一棵与或树，其特点是：

①博弈的初始状态是初始节点；

②博弈树中的“或”节点和“与”节点逐层交替出现。

③整个博弈过程始终站在某一方的立场上，所有能使自己一方获胜的终局都是本原问题，相应的节点是可解节点；所有使对方获胜的终局都是不可解节点。

1  2  3  4