三、α-β剪枝技术
下面学习α-β剪枝技术
1.α-β剪枝技术的思想
极大极小过程是先生成与/或树,然后再计算各节点的估值,即生成节点和计算估值这两个过程是分离的。在搜索时,需要生成规定深度内的所有节点,因此搜索效率较低。
以棋盘为15×15大小的五子棋为例,人机对弈,用极大极小搜索算法,搜索深度为3时,计算机(配置:CUP赛场1.7G,内存DDR266 256M)每走1步要用10min,搜索的节点数超过了107个;而搜索深度为4时,每走1步要用10个多小时,搜索节点数超过了2×109个。
如果能边生成节点边对节点估值,并根据一定的条件,提前剪去一些没用的分枝,那么就可以有效提高搜索效率。在这种思想的基础上,人们提出了α-β剪枝技术。
采用有界深度优先策略,当生成规定深度的节点时,计算叶节点的静态估值,并倒推非端节点的估值。根据倒推结果,在非端节点的向下分枝中,剪掉那些目前未知,但无论如何都不会改变非端节点倒推值的未扩展分枝。
用α-β剪枝技术,搜索深度为3时,每走1步不到2min,搜索的节点数小于1.5×106个;而搜索深度为4时,每走1步要用160min,搜索的节点数小于2×108个。
2.α-β剪枝技术
作为正方出现的MAX节点,假设它的MIN子节点有N个,那么当它的第一个MIN子节点的评估值为a时,则对于其它的子节点,如果有高过a的,就取那最高的值作为该MAX节点的评估值;如果没有,则该MAX节点的评估值为a。
总之,该MAX节点的评估值不会低于a,这个a就称为该MAX节点的评估下限值。
作为反方出现的MIN节点,假设它的MAX子节点有N个,那么当它的第一个MAX子节点的评估值为b时,则对于其它子节点,如果有低于b的,就取那个低于b的值作为该MIN节点的评估值;如果没有,则该MIN节点的评估值取b。
总之,该MIN节点的评估值不会高过b,这个b就称为该MIN节点的评估上限值。
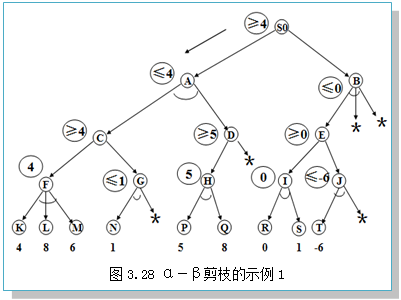
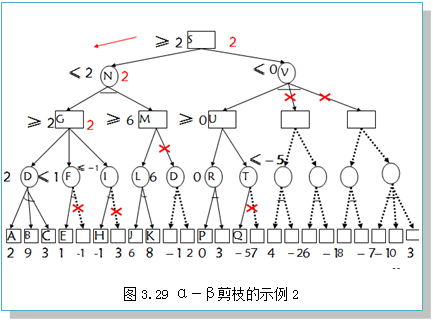
①α剪枝:若任一MIN节点(“与”节点)的β值小于或等于其父节点(MAX节点(“或”节点))的α值(即不能升高其父节点的α值),则可中止该MIN节点以下的搜索过程。这个MIN节点最终的倒推值就设定为这个β值。
②β剪枝:若任一MAX节点(“或”节点)的α值大于或等于其父节点(MIN节点(“与”节点))的β值(即不能降低其父节点的β值),则可以中止该MAX节点以下的搜索过程。这个MAX节点最终的倒推值就设定为这个α值。
图3.28和图3.29给出了两个α-β剪枝的示例。