您的当前位置是：第三章 确定性推理>>学习内容>>知识点四

二、极大极小搜索过程

一盘棋平均走50步，总状态数约为10的161次方。假设1毫微秒走一步，约需10的145次方年。结论：不可能穷举。

1．对各个局面进行评估

①评估的目的：对后面的状态提前进行考虑，并且以各种状态的评估值为基础作出最好的走棋选择。

②评估的方法：用评价函数对棋局进行评估。赢的评估值设为+∞，输的评估值设为-∞，平局的评估值设为0。

③评估的标准：由于下棋的双方是对立的，只能选择其中一方为评估的标准方。

2．MAX节点和MIN节点

命名博弈的双方，一方为“正方”，对每个状态的评估都是对应于该方的输赢的。例如，赢2个，输1个等，都是指正方的。正方每走一步，都在选择使自己赢得更多的节点，因此这类节点称为“MAX”节点；

另一方为“反方”，对每个状态的评估都是对应于对手的输赢的。例如，赢2个，输一个，其实是指自己输2个，赢1个的。反方每走一步，都在选择使对手输得更多的节点，因此这类节点称为“MIN”节点。

由于正方和反方是交替走步的，因此MAX节点和MIN节点会交替出现。

3．极大极小分析法的基本思想

设博弈的双方中一方为MAX，另一方为MIN。然后为其中的一方（例如MAX）寻找一个最优行动方案。为了找到当前的最优行动方案，需要对各个可能的方案所产生的后果（得分）进行比较。为计算得分，需要根据问题的特性信息定义一个估价函数，用来估算当前博弈树端节点的得分。当端节点的估值计算出来后，再推算出父节点的得分。推算的方法是：

①对“或”节点，选其子节点中一个最大的得分作为父节点的得分，这是为了使自己在可供选择的方案中选一个对自己最有利的方案；

②对“与”节点，选其子节点中一个最小的得分作为父节点的得分，这是为了立足于最坏的情况。

如果一个行动方案能获得较大的倒推值，则它就是当前最好的行动方案。

4．静态估计函数

极小极大搜索策略是考虑双方对弈若干步之后，从可能的走步中选一步相对好棋的走法来走，即在有限的搜索深度范围内进行求解。为此要定义一个静态估计函数f，以便对棋局的势态（节点）作出优劣估值，这个函数可根据势态优劣特征来定义（主要用于对端节点的“价值”进行度量）。一般规定:

①有利于MAX的势态，f（p）取正值；

②有利于MIN的势态，f（p）取负值；

③势均力敌的势态，f（p）取0值。

若f（p）＝＋∞，则表示MAX赢；

若f（p）＝－∞，则表示MIN赢。

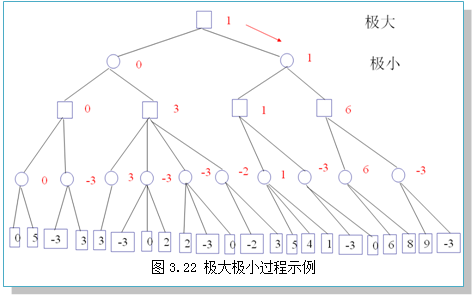
5．极大极小过程步骤

下面的讨论规定：

顶节点深度d＝0，MAX代表程序方，MIN代表对手方，MAX先走。

极大极小过程步骤：

①以当前考察的态势P为根节点，生成指定深度的博弈树。

②根据静态估计函数f计算各叶节点的估计值。

③自底向上计算各个非叶节点的估计值，计算的方法是MAX节点取其子节点的最大值，MIN节点取其子节点的最小值。

④将根节点的倒推值对应的策略作为当前的最佳策略。

图3.22给出了一个极大极小过程示例。

1  2  3  4