您的当前位置是:第三章 确定性推理>>学习内容>>知识点四


例3.7 一字棋游戏
下面学习案例——一字棋游戏
设有一个行三列的棋盘,两个棋手轮流走步,每个棋手走时往空格上摆一个自己的棋子,谁先使自己的棋子成三子一线为赢。设程序方MAX的棋子用(a)表示,对手MIN的棋子用(b)表示,MAX先走。用极大极小搜索方法为MAX寻找第一步棋的最佳走法。(搜索深度为2)
静态估计函数f(p)规定如下:
①若P是MAX的必胜局,则f(P)=+∞;
②若P是MIN的必胜局,则f(P)=-∞;
③若P对MAX、MIN都是胜负未定局,则
f(P)=e(+P)-e(-P)
其中,e(+P)表示棋局P上有可能使a成三子一线的数目;e(-P)表示棋局P上有可能使b成三子一线的数目。
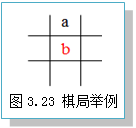
如图3.23所示的棋局,估计函数的计算过程为:
e(+P)=4,e(-P)=6,f(P)=e(+P)-e(P)=-2
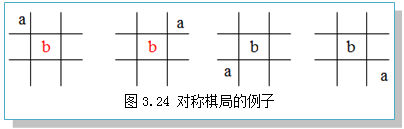
在搜索过程中,具有对称性的棋局认为是同一棋局,以大大减少搜索空间。如图3.24所示的4个棋局是对称的棋局。
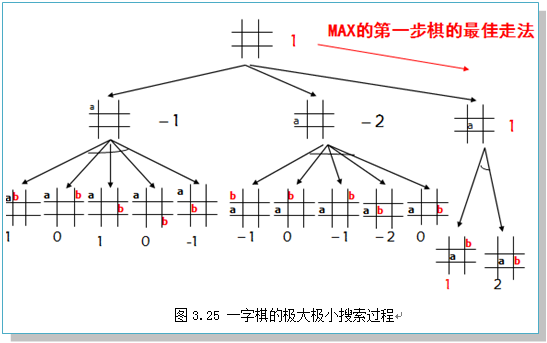
该问题的极大极小搜索过程如图3.25所示。
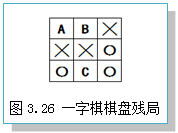
例3.8 一字棋棋盘残局。
设有一个摆放三个子的棋盘残局,如图3.26所示,〇和╳在结束前有三步棋可以走,而且设走第一步的是╳。这时存在着三个空格A,B,C,用极大极小过程判断应该把棋子放到哪一格内。(搜索深度为2)
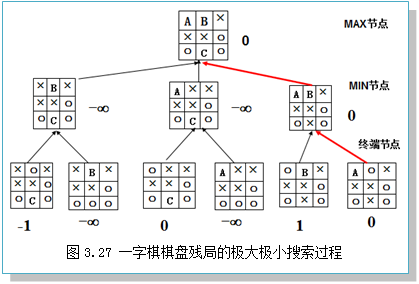
问题的极大极小搜索过程如图3.27所示,对于棋盘残局中的╳来说,最好的选择,是将╳放在C的位置上,这时可以导致平局局面。