2．消解反演
下面继续学习消解原理
设S是子句集，c是子句。若存在一个子句序列c1，…，cn满足
①cn=c；
②任意一个ci或者属于S或者它前面的子句ck，cl（i>k，i>l）的消解式；
则称c1，…，cn是从子句集S到子句c的一个消解演绎；当 c=NIL时的消解演绎称为（消解）反演。
反演的基本算法如下，其流程图如图3.30所示。
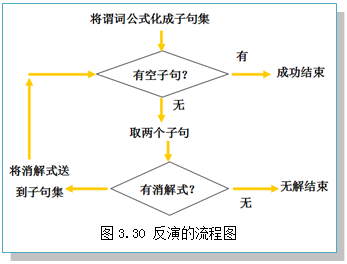
①把谓词公式转化为子句集S（所有子句的变量名不同）；
②如空子句成为子句集的子句，则算法结束；
③在子句集中选取两个不同的可以消解的子句ci，cj；
④计算ci，cj的消解式rij；
⑤把rij加到子句集中，形成新的子句集S；
⑥转到②。
例3.11
设子句集为S={P∨Q，～P∨Q，P∨～Q，～P∨～Q}求S的一个反演。
S的一个反演如下：
①P∨Q （S）
②～P∨Q （S）
③P∨～Q （S）
④～P∨～Q （S）
⑤Q ①②
⑥～Q ③④
⑦NIL ⑤⑥
反演过程不唯一，还可以给出S的另一个反演如下：
⑤P ①③
⑥～P ②④
⑦NIL ⑤⑥
例3.12
设S={
～P（z1，a）∨～P（z1，x1）∨～P（x1，z1），
P（z2，f（z2））∨P（a，z2），
P（f（z3），z3）∨P（a，z3） }
求S的一个反演。
反演过程：
①～P（z1，a）∨～P（z1，x1）∨～P（x1，z1） （S）
②P（z2，f（z2））∨P（a，z2） （S）
③P（f（z3），z3）∨P（a，z3） （S）
④P（a，f（a）） （①②），ß={a/x1，a/z1，a/z2}
⑤P（f（a），a） （①③），ß={a/x1，a/z1，a/z3}
⑥～P（f（a），a） （①④）ß={a/x1，f（a）/z1}
⑦NIL （⑤⑥）
3．消解推理规则
命题的特殊情况：
①假言推理
父辈字句P ～P∨Q（即P=>Q）
消解式Q
②合并
父辈字句P∨Q ～P∨Q
消解式Q∨Q=Q
③重言式
父辈字句P∨Q ～P∨～Q
消解式Q∨～Q
P∨Q ～P∨～Q
P∨～P
④空子句（矛盾）
～P P
NIL
⑤链式（三段论）
～P∨Q，（即P=>Q） ～Q∨R，（即Q=>R）
～P∨R，（即P=>R）
含有变量的消解式（谓词情况）
例3.13
1．
B（x） ～B（y）∨C（y）
置换σ={x/y}
C（x）
2．
P（x）∨Q（x） ～Q[f（y）]
置换σ={f（y）/x}
P[f（y）]
3．
P[x，f（y）]∨Q（x）∨R[f（a），y] ～P[f（f（a）），z]∨R（z，w）
σ={f（f（a））/x，f（y）/z}
Q[f（f（a））]∨R[f（a），y]∨R[f（y），w]
4．消解反演求解过程
消解反演证明定理的思路非常类似于数学中的反证法。
给定一个公式集S（前提条件）和目标公式L（结论），通过反演来求证目标公式L，其证明过程为：
①否定L，得到～L；
②把～L加到S中；
③把新形成的集合{S，～L}化为子句集；
④应用消解原理，试图导出一个表示矛盾的空子句。
