下面继续学习消解原理
例3.14
设有公式集：
F1:（
x）（C（x）=>（W（x）∧R（x））
F2:（
x）（C（x）∧O（x））
L:（x）（O（x）∧R（x））
试证：L是F1，F2的逻辑结果，即F1∧F2=>L。
证明：首先分别求出F1，F2和～L的子句集。
F1的前束合取范式与子句集：
（x）（C（x）=>（W（x）∧R（x））
①（x）（～C（x）∨（W（x）∧R（x））
②③④⑤⑥（x）（（～C（x）∨W（x））∧（～C（x）∨R（x）））
⑦⑧子句集={～C（x）∨W（x），～C（x）∨R（x）}
⑨子句集={～C（x1）∨W（x1），～C（x2）∨R（x2）}
F2的前束合取范式和子句集：
（x）（C（x）∧O（x））
①②③④x=a
（C（a）∧O（a））
⑤⑥⑦⑧⑨子句集={ C（a），O（a）}
～L的前束范式和子句集：
～（x）（O（x）∧R（x））
①②（x）（～O（x）∨～R（x））
③④⑤⑥⑦⑧⑨子句集={～O（x）∨～R（x）}
构成子句集（注意各子句的变量不重名）
{～C（x1）∨W（x1），～C（x2）∨R（x2），C（a），O（a），～O（x）∨～R（x）}
消解过程：
①～C（x1）∨W（x1）
②～C（x2）∨R（x2）
③C（a）
④O（a）
⑤～O（x）∨～R（x）
⑥R（a） ②③，mgu={a/x2}
⑦～R（a） ④⑤，mgu={a/x}
⑧NIL ⑥⑦
例3.15
用消解反演证明：
前提：每一个储蓄钱的人都获得利息
结论：如果没有利息，那么就没有人去储蓄钱
证明：
设
S（x，y）：某人x储蓄y
M（x）：x是钱
I（x）：x是利息
E（x，y）：某人x获得y
前提：每一个储蓄钱的人都获得利息
（x）{[（y）（S（x，y）∧M（y））] =>[（y）（I（y）∧E（x，y））]}
结论：如果没有利息，那么就没有人去储蓄钱
～（x）I（x）=>（x）（y）（M（y）=>～S（x，y））
前提化成子句集：
（x）（～（y）（S（x，y）∧M（y））∨（y）（I（y）∧E（x，y）））
=（x）（（y）（～S（x，y）∧M（y）））∨（y）（I（y）∧E（x，y）））
=（x）（（y）（～S（x，y）∨～M（y））∨（y）（I（y）∧E（x，y）））
=（x）（（y）（～S（x，y）∨～M（y））∨（z）（I（z）∧E（x，z）））改名
z=f（x）斯科伦函数
=（x）（（y）（～S（x，y）∨～M（y））∨（I（f（x））∧E（x，f（x））））
=（x）（y）（（～S（x，y）∨～M（y））∨（I（f（x））∧E（x，f（x））））
=（x）（y）（（～S（x，y）∨～M（y）∨I（f（x））∧（～S（x，y）∨～M（y）∨E（x，f（x）））
（x）（y）（（～S（x，y）∨～M（y）∨I（f（x））∧（～S（x，y）∨～M（y）∨E（x，f（x）））
前提条件的子句集
①～S（x，y）∨～M（y）∨I（f（x））
②～S（u，v）∨～M（v）∨E（u，f（u））
结论取非：
～（～（x）I（x）=>（x）（y）（M（y）=>～S（x，y）））
结论的非化成子句集
～（（x）I（x）∨（x）（y）（～S（x，y）∨～M（y）））
=（～（x）I（x）∧（～（x）（y）（～S（x，y）∨～M（y））））
=（（x）～I（x）∧（（x）（y）（S（x，y）∧M（y））））
=（（z）～I（z）∧（S（a，b）∧M（b）））
=（z）（～I（z）∧S（a，b）∧M（b））
“结论非”的子句集
③～I（z）
④S（a，b）
⑤M（b）
消解过程如下：
①～S（x，y）∨～M（y）∨I（f（x））
②～S（u，v）∨～M（v）∨E（u，f（u））
③～I（z）
④S（a，b）
⑤M（b）
⑥～S（x，y）∨～M（y） ①③ mgu={f（x）/z}
⑦～M（b） ④⑥ mgu={a/x，b/y}
⑧NIL ⑤⑦
消解反演除了证明定理之外，还可以用来求解问题，其方法与定理证明类似。
步骤：
①把已知前提用谓词公式表示出来，并化为相应的子句集S；
②把目标公式的否定产生的每个子句添加到目标公式否定之否定的子句中，得到重言式；
③按反演树执行消解，直至根部得到某个子句为止；
④用根部的子句作为一个回答语句。
答案求取涉及到把一棵根部有NIL的反演树变换为在根部带有可用作答案的某个语句的一棵证明树。
例3.16
“如果无论约翰（John）到哪里去，菲多（Fido）也就去那里，那么如果约翰在学校里，菲多在哪里呢？”
这个问题说明了两个事实，然后提出一个问题，而问题的答案大概可从这两个事实推导出。
设：AT（x，y）:x在y处。
这两个事实可以解释为下列公式集S：
（x）[AT（JOHN，X）=>AT（FIDO，X）]和AT（JOHN，SCHOOL）
目标公式（x）AT（FIDO，x）
其否定为～（x）AT（FIDO，x）
即：（x）[～AT（FIDO，x）]
所得子句为～AT（FIDO，x）
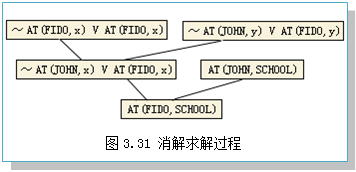
其消解求解过程如图3.31所示。
