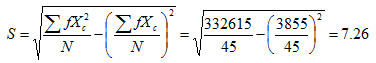当前位置:课程学习>>第三章>>知识讲解>>视频课堂>>知识点四
知识点四:方差与标准差
我们通过上述视频深入了解了全距的概念、方差与标准差的概念与适用情况及其计算方法。现在我们来进行归纳总结:
全距又叫极差,是指一组观测值中,最大数值与最小数值之差,用符号![]() 表示,即
表示,即![]() 。
。
方差是一组数据离差平方和的平均数,也叫变异数。方差的算术平方根称为标准差。方差和标准差是最常用的描述数据分布离散程度的差异量数,反映了各变量值与均值的平均差异。总体方差用符号![]() 表示,样本方差用符号
表示,样本方差用符号![]() 表示。定义公式分别为:
表示。定义公式分别为:![]() 和
和![]()
总体标准差用符号![]() 表示,样本标准差用S表示。公式为
表示,样本标准差用S表示。公式为
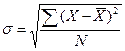 和
和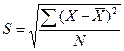
式中,![]() 为原始观测值;
为原始观测值;![]() 为平均数
为平均数
为了计算方便,可直接使用原始观测值计算标准差,公式为:
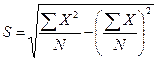
式中,![]() 为标准差,
为标准差,![]() 为原始观测值,
为原始观测值,![]() 为观测值个数
为观测值个数
分组资料求标准差,同分组资料求平均数一样,用组中值做为各组数据的代表值,计算公式为:
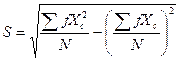
式中,![]() 表示组中值,
表示组中值,![]() 表示各组对应的次数,
表示各组对应的次数,![]() 为总次数。
为总次数。
标准差的适用条件主要有:一组数据的一般水平适合算术平均数描述时,其离散程度宜用标准差来描述;进一步参与其他运算时。如计算差异系数、相关系数等其他统计量;在推断统计,尤其在方差分析时,常用方差表示数据的离散程度。
边学边练
- 1.某班45名学生的语文成绩如下表,求分析这45名学生成绩的差异情况。【简答题】。
-
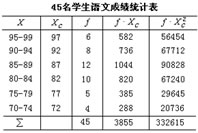
接下来我们进入学以致用