当前位置：课程学习>>第四章>>知识讲解>>视频课堂>>知识点五
知识点五：总体平均数与总体比率的区间估计
我们通过上述视频深入了解了总体平均数的区间估计、总体比率的区间估计。现在我们来进行归纳总结：
总体正态分布，总体标准差已时，样本平均数抽样分布服从正态分布，样本平均数与总体平均数的差异为
。
总体正态分布，总体标准差未知时：1．当n≥30时，平均数的抽样分布为渐进正态分布，用样本标准差
代替总体标准差
，所以总体平均数置信度为0.95的置信区间为（
，
）；置信度为0.99的置信区间为（
，
）。2．当n<30时，样本平均数的抽样分布为t分布，某一可靠度下总体平均数的区间估计要依据t分布来进行。
可以通过t值表查出，
的置信度为1-α的置信区间为：
下置信界限：
上置信界限：
总体非正态分布时，无论总体方差已知与否，当总体非正态分布时，只有样本容量n≥30时，才能用样本平均数的抽样分布理论来估计总体平均数。由于此时样本平均数的抽样分布近似正态分布，所以可采用正态分布理论对总体平均数进行区间估计。
边学边练
- 1.从某正态总体中随机抽取
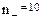和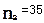
的两个样本，分别求得
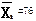和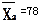
，已知总体标准差
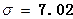，试估计总体平均数
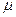在0.95和0.99置信度下的置信区间。【简答题】。
-
，故应用正态分布理论进行估计。依题
，
用- 2.从某年级随机抽取50人，某学科测验的平均成绩为80分，标准差为5.6分。已知该学科历年测验成绩均服从正态分布。试估计该年级该学科的平均成绩的0.95和0.99的置信区间。【简答题】。
-
，故
0.95的置信区间为80—1.96╳0.79< 接下来我们进入学以致用
