第六章 统计假设检验(下)
 知识点四:
知识点四: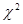 检验
检验
案例:某中学校长发现高一学生对高中学习目标很模糊,对自己的中学生涯不会规划和设计,于是想从高一开始设置中学生生涯设计校本课程。从全校教师中随机抽取30名,征求他们的意见。结果同意者为17人,不置可否者3人,不同意者10人。然后又了解家长的意见,随机抽取了162名学生家长进行了调查,结果如下。问教师的调查结果能否说明为高一学生开始中学生生涯设计课程的意见占优势?另外,学生家长的社会阶层与其对课程改革的态度是否有关系?
这一问题的分析,一方面是分析调查对象对某个事情的观点在次数分布上是否一致,另一方面是按两个分类标志各分为若干组的资料,分析这两个分类标志间是否独立。这需要一种新的检验方法,即![]() 检验。
检验。
一、![]() 检验与
检验与![]() 分布
分布
![]() (读作卡方)检验法是非参数检验法,特别是检验计数资料最常用的方法。
(读作卡方)检验法是非参数检验法,特别是检验计数资料最常用的方法。![]() 检验是用来检验按属性分类的计数资料实际观察次数分布与理论分布是否相符合的统计方法,也可以用于同一资料按两个分类标志各分为若干组的资料中,检验两种分类标志下的现象间是否彼此独立。适用条件为样本随机抽取;各属性间是均匀分布、相互独立;最好总体远大于样本。检验公式为:
检验是用来检验按属性分类的计数资料实际观察次数分布与理论分布是否相符合的统计方法,也可以用于同一资料按两个分类标志各分为若干组的资料中,检验两种分类标志下的现象间是否彼此独立。适用条件为样本随机抽取;各属性间是均匀分布、相互独立;最好总体远大于样本。检验公式为:![]()
![]()
式中,![]() 为实际观察次数;
为实际观察次数;![]() 为理论次数
为理论次数
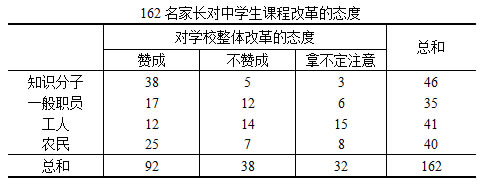
![]() 检验所依据的分布是
检验所依据的分布是![]() 分布。
分布。![]() 的抽样分布形态呈正偏态,右侧无限延伸,但永不与基线相交,并随自由度的变化而变化。自由度越小,
的抽样分布形态呈正偏态,右侧无限延伸,但永不与基线相交,并随自由度的变化而变化。自由度越小,![]() 分布的偏斜度越大,随着自由度的不断增加,
分布的偏斜度越大,随着自由度的不断增加,![]() 曲线与正态分布接近,当自由度趋向于无穷时,
曲线与正态分布接近,当自由度趋向于无穷时,![]() 曲线为正态曲线。
曲线为正态曲线。
从公式可以看出,![]() 值总是非负的,具有可加性,它是反映实际观察次数与理论次数差异程度的统计量。当实际次数与理论次数间的差异越小,
值总是非负的,具有可加性,它是反映实际观察次数与理论次数差异程度的统计量。当实际次数与理论次数间的差异越小,![]() 值就越小,表明实际观察次数与理论次数的一致性程度越高;当差异为0时,
值就越小,表明实际观察次数与理论次数的一致性程度越高;当差异为0时,![]() 值为0;
值为0;![]() 值越大,表明实际观察次数与理论次数之间的一致性程度越低。
值越大,表明实际观察次数与理论次数之间的一致性程度越低。
![]() 检验的步骤为:(1)提出假设;(2)确定理论次数
检验的步骤为:(1)提出假设;(2)确定理论次数![]() ;(3)求
;(3)求![]() 值;(4)确定α水平,并查表确定理论
值;(4)确定α水平,并查表确定理论![]() 值。(5)统计决断。如果
值。(5)统计决断。如果![]() ≥
≥![]() ,则拒绝原假设,接受备择假设,否则保留原假设。
,则拒绝原假设,接受备择假设,否则保留原假设。
二、![]() 检验的吻合性检验
检验的吻合性检验
案例中分析教师对赞成开设中学生生涯设计课程的意见是否占优势,实际上是分析实际获得的观测值的分布与理论上的分布差异是否显著。这一问题就![]() 的吻合性检验,即对于一组观测值,按某一属性标志分为两组或两组以上,检验各组实际分布与理论分布或某规则是否相吻合。
的吻合性检验,即对于一组观测值,按某一属性标志分为两组或两组以上,检验各组实际分布与理论分布或某规则是否相吻合。![]() 检验中,确定理论次数的依据是原假设。主要有两种情况:一种是原假设为各组间无差异,这时各组理论次数相等。如案例中假定教师对开设中学生生涯设计课程各态度人数相等,则男赞成、不赞成和不置可否的人数都是10;第二种是按某一理论分布提出假设,如假设某资料服从正态分布,则理论次数应按相应的理论或原则计算。吻合性检验的自由度为df=组数-1。
检验中,确定理论次数的依据是原假设。主要有两种情况:一种是原假设为各组间无差异,这时各组理论次数相等。如案例中假定教师对开设中学生生涯设计课程各态度人数相等,则男赞成、不赞成和不置可否的人数都是10;第二种是按某一理论分布提出假设,如假设某资料服从正态分布,则理论次数应按相应的理论或原则计算。吻合性检验的自由度为df=组数-1。
对于案例中提到的第一个问题,解答如下:
假设教师对开设中学生生涯设计课程持赞成、不可置否、反对意见的人数相等,则理论次数为![]()
所以![]()
![]()
![]()
取α=0.01,df=3-1=2。查![]() 分布表,则
分布表,则![]() (0.01)2=9.210。因此,拒绝原假设,接受备择假设,结论为:教师对开设中学生生涯设计课程的意见差异显著,同意开设的占优势。
(0.01)2=9.210。因此,拒绝原假设,接受备择假设,结论为:教师对开设中学生生涯设计课程的意见差异显著,同意开设的占优势。
再如某小学报告该校三年级学生的阅读成绩,90~100分、80~89分、70~79分、60~69分以及60分以下者的比例为:2∶4∶8∶5∶1。现从该校三年级中随机抽取60名学生的阅读成绩,90分以上者为5名,80~89分的为16名,70~79分的为21名,60~69分的为14名,60分以下者为4名。根据这一调查资料,推断该校报告的比例是否可靠。
解:假设该校报告的比例可靠,那么各成绩水平的学生比例应为:2∶4∶8∶5∶1,则各级分数的理论人数分别为:
90分以上:![]() ;80分以上:
;80分以上:![]() ;70分以上:
;70分以上:![]() ;
;
60分以上:![]() ;60分以下:
;60分以下:![]() 。所以
。所以
![]()
![]()
![]()
确定α水平和自由度。取α=0.05,df=5-1=4。查![]() 分布表,得
分布表,得![]() (0.05)4=9.488。
(0.05)4=9.488。
由于计算的![]() =2.275<
=2.275<![]() (0.05)4=9.488,所以保留原假设,拒绝备择假设,认为该校报告的成绩比例是可靠的。
(0.05)4=9.488,所以保留原假设,拒绝备择假设,认为该校报告的成绩比例是可靠的。
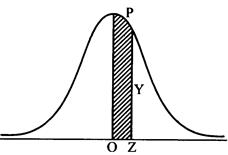
某中学校随机抽取初二学生150名,对他们进行注意力调查,结果分为优、良、中、差四等。调查结果,其中优18名,良59名,中60名,差13名。问这一调查结果是否服从正态分布?
解:假定该调查结果服从正态分布。查正态分布表,依正态曲线下面积比率确定各等级的理论人数。则各等级的人数为:
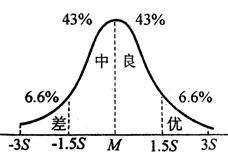
优位于Z=1.5以上区间,面积比率为0.5-0.43319=0.0668,人数为150×0.0668=10;
良位于Z=0—1.5之间,面积比率为0.43319,人数为150×0.43319=65;
中位于Z=-1.5—0之间,面积比率与良对称,人数为150×0.43319=65;
差位于Z=1.5以下的区间,面积比率与优对称,人数为150×0.0668=10;
所以![]()
![]()
![]()
![]()
取α=0.05,df=4-1=3。查![]() 分布表得:
分布表得:![]() (0.05)3=7.81,由于计算的
(0.05)3=7.81,由于计算的![]() =8.24>
=8.24>![]() (0.05)3=7.81,所以拒绝原假设,接受备择假设,结论为调查结果学生注意力各等级间差异显著,不服从正态分布。
(0.05)3=7.81,所以拒绝原假设,接受备择假设,结论为调查结果学生注意力各等级间差异显著,不服从正态分布。
二、![]() 独立性检验
独立性检验
案例中,对家长的分类,一方面按阶层分四类,另一方面按对开设中学生生涯设计课程的态度分三类。对这类数据所进行的检验是![]() 独立性检验,即检验这两个分类标志间是否独立。把一个标志的资料写在行内,另一个标志写在列内,这样的表格在统计上称为列联表,自由度为df=(行数-1)(列数-1)=(r-1)(k-1),(其中,r表示行数, k表示列数)。
独立性检验,即检验这两个分类标志间是否独立。把一个标志的资料写在行内,另一个标志写在列内,这样的表格在统计上称为列联表,自由度为df=(行数-1)(列数-1)=(r-1)(k-1),(其中,r表示行数, k表示列数)。
![]() 独立性检验中,原假设为两个分类标志是独立的。在此假设下,列联表中每一小格的理论次数为
独立性检验中,原假设为两个分类标志是独立的。在此假设下,列联表中每一小格的理论次数为
![]()
如果观察或实验得到的计数资料是按两个属性分类,且每种属性下又分为两类时,就形成了2×2列联表,这种列联表也叫四格表,其自由度为1。如某中学随机抽取高二男生60名,女生50名,进行理化测验。分析学生理化成绩及格情况是否与性别有关。
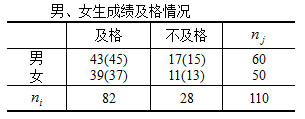
假设成绩及格情况与性别无关。各格的理论次数为:
男生及格:![]() ,不及格:
,不及格:![]()
女生及格:![]() ,不及格:
,不及格:![]() 所以,
所以,
![]()
![]()
![]()
取α=0.05,df=1,查![]() 分布表,
分布表,![]() 0.05(1)=3.84。由于计算的
0.05(1)=3.84。由于计算的![]() =0.77<
=0.77<![]() 0.05(1)=3.84,所以拒绝原假设,认为理化成绩及格情况与性别无关。
0.05(1)=3.84,所以拒绝原假设,认为理化成绩及格情况与性别无关。
对于2×2列联表求![]() 值,也可以采用简捷方法:
值,也可以采用简捷方法:![]()
![]()
式中,N为观测值总次数;![]() 、
、![]() 、
、![]() 、
、![]() 分别表示四格表中各格实际观察次数
分别表示四格表中各格实际观察次数
案例中提到的家长对学校课程改革的态度调查是一个![]() 列联表,分析如下:
列联表,分析如下:
原假设为家长对改革的态度与他们所属的阶层没有关系。各格的理论次数为:
![]() ;
;![]() ;
;![]() ,
,![]() ;
;![]() ;
;![]() ,同理可求得:
,同理可求得:![]() ;
;![]() ;
;![]() ,
,![]() ;
;![]() ;
;![]()
![]()
![]()
![]()
自由度为df=(r-1)(k-1)=(4-1)(3-1)=6,取α=0.05。查![]() 分布表得:
分布表得:![]() 0.05(6)=16.81。由于计算的
0.05(6)=16.81。由于计算的![]() =28.89>
=28.89>![]() 0.05(6)=16.81,所以拒绝原假设。结论为学生家长对小学整体改革的态度与其所属的社会阶层有极其密切的关系。
0.05(6)=16.81,所以拒绝原假设。结论为学生家长对小学整体改革的态度与其所属的社会阶层有极其密切的关系。
