第七章 相关分析
 知识点四:点二列相关与
知识点四:点二列相关与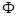 相关
相关
一、点二列相关
有些变量的测控结果只有两个类别,如男与女、成功与失败、是与非、对与错、已婚与未婚,象这样的按事物某一属性划分只有两类结果的变量称为二分称名变量,简称二分变量。二分变量分为真正的二分名义变量和人为的二分名义变量。真正的二分名义变量是指按照事物性质划分为两类的变量,如男与女。人为的二分变量是指变量本来是连续的,被某种人为规定的标准分为两个类别,如按一定标准将属于正态连续变量的学科考试分数划分为及格与不及格、录取与未录取、通过与未通过等。
如果求相关的两列变量中,其中一个变量是正态连续变量,而另一个变量是真正的二分称名变量,描述这样两个变量之间相关程度的方法称为点二列相关,用符号![]() 表示,计算公式为:
表示,计算公式为:![]()
式中,![]() 与
与![]() 分别为二分变量中各自占总体的比例,
分别为二分变量中各自占总体的比例,![]() +
+![]() =1;
=1;![]() 为连续变量中与
为连续变量中与![]() 对应部分的平均数;
对应部分的平均数;![]() 为连续变量中与
为连续变量中与![]() 对应部分的平均数;
对应部分的平均数;![]() 为连续变量全部观测值的标准差。
为连续变量全部观测值的标准差。
点二列相关常用于检验一个测验中,二分变量对连续变量的影响,是考试质量分析的重要方法,多用于客观性测验时评价测验内部的一致性、鉴定试卷题目的区分度等。其计算步骤为:
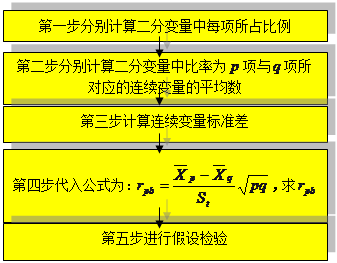
语文统考试卷第1题的区分度,即16名初三学生语文期末统考第1题得分与总分相关程度计算过程为:
设答对第1题的人数比例为![]() ,答错的人数比例为
,答错的人数比例为![]() ,则依据数值求得:
,则依据数值求得:![]() =0.5624,
=0.5624,![]() =1-
=1-![]() =0.4375,
=0.4375,![]() =87,
=87,![]() =75.1,
=75.1,![]() =11.11,
=11.11,
![]() =
=![]() ==
==![]() 0.53
0.53
点二列相关系数的检验,可以采用查积差相关系数显著性临界值法(点二列相关是积差相关的一种特殊形式)。即在一定的![]() 水平下按
水平下按![]() =
=![]() -2查积差相关系数临界值表,
-2查积差相关系数临界值表,![]() 为求点二列相关时连续变量的个数。如果实际求得的
为求点二列相关时连续变量的个数。如果实际求得的![]() ,说明
,说明![]() 与零相关差异显著,否则就说明样本来自一个零相关的总体。
与零相关差异显著,否则就说明样本来自一个零相关的总体。
计算的![]() =0.53,n=16,
=0.53,n=16,![]() ,
,![]() =0.497,
=0.497,![]() >
>![]() ,所以
,所以![]() =0.53有意义,第1题与总分的相关程度为中度相关,该题的区分度为中度区分。
=0.53有意义,第1题与总分的相关程度为中度相关,该题的区分度为中度区分。
另外,也可以采用两个独立样本平均数间差异的检验法(第六章的内容)进行显著性检验,即对![]() 和
和![]() 的差异进行检验。
的差异进行检验。
二、![]() 相关
相关
某校随机抽取初二学生期末语文试卷30份,其中第1题为是非判断题,30名学生每人的考试总分以及在第1题上的对错情况如下表。现以60分作为及格线,问第1题对错情况与及格与否是否相关。
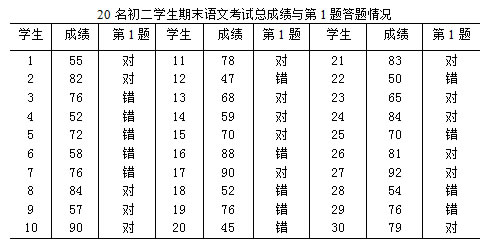
试题对和错只有两种情况,而成绩及格和不及格也是两种情况,像这样描述两列变量均为二分名义变量的相关程度用![]() (读phi)相关,用符号
(读phi)相关,用符号 ![]() 表示。
表示。![]() 相关要求同一组资料按两个标志分类,且每个标志下只有两个点值,表明变量的某种属性,如男与女、对与错、录取与不录取等,并把资料整理成2×2列联表的形式。计算公式为:
相关要求同一组资料按两个标志分类,且每个标志下只有两个点值,表明变量的某种属性,如男与女、对与错、录取与不录取等,并把资料整理成2×2列联表的形式。计算公式为:
![]() =
=![]()
式中, a、b、c、d 各代表四格表中每格的实际次数
先将这30名学生的及格情况与第1题答题情况整理成四格表。
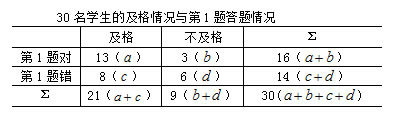
所以![]() =
=![]() =
=![]() =0.26
=0.26
然后对![]() =0.26进行假设检验。
=0.26进行假设检验。![]() 系数的显著性检验主要是
系数的显著性检验主要是![]() 检验,即看同一资料的
检验,即看同一资料的![]() 值是否达到一定的显著性水平。
值是否达到一定的显著性水平。![]() 与
与![]() 值间的关系为:
值间的关系为:![]() =
=![]() 。如果求得的
。如果求得的![]() 值达到一定的显著水平,即
值达到一定的显著水平,即![]()
![]()
![]() ,则说明
,则说明![]() 与零相关有显著差异;如果
与零相关有显著差异;如果![]() <
<![]() ,则说明
,则说明![]() 与零相关没有显著差异。
与零相关没有显著差异。
由于![]() =0.26,N=30,所以
=0.26,N=30,所以![]() =
=![]() ,
,![]() ,
,![]() ,P<0.01,因此,拒绝原假设,
,P<0.01,因此,拒绝原假设,![]() 有意义。
有意义。
