人的心理特质水平经测量之后应表现为一个数值。然而，由于测量误差的存在，实际测得的数值往往难以和该特质的真实水平完全一致，它总会略高于或略低于其真实水平值，某些时候还会严格偏离其真实水平值。例如，我们平常所说的“××考生基本上考出了其应有水平”或“××人这次测验超水平发挥”等等，就是对这种测量现象的一种描述。为研究方便，我们把反映被试某种心理特质真正水平的那个数值称作该特质的真分数（True Score，简称为T分数），比如在教育测验中考生的真实的能力水平；把实际测量得到的分数称作为该特质的观察分数（Observed Score）。当观察分数接近真分数时，就说这次测量的误差较小。

显然，真分数是一个在理论上构想出来的抽象概念，在实际测量中试很难得到的。因为任何一种测量，无论它有多么科学，总会存在误差。我们只能通过改进测量工具，完善操作方法等办法来使观察值尽量接近真分数。只要观察分数与真分数之间的误差不是太大，或者说误差被控制在可接受的范围之内，我们的测量也就可以看作是可接受的测量了。

经典测量理论（CCT）是以真分数理论（True Score Theory）为核心假设的测量理论及其方法体系，也称真分数理论（True Score Theory），是心理和教育测量学发展历史中最早实现数学形式化的测量理论。十九世纪初经过斯皮尔曼(Spearman)等人的应用和研究有所发展，后经几十年的不断实践、改进，而日趋丰富、完善，使之形成一种具有数十种项目分析指标及评价标准体系的测试理论。

自比奈编制测量理论以来，经典测验理论历经百年发展，围绕着实得分数与真分数和误差分数的关系已经建立起一套完整的测量理论与统计分析方法，是当前占据统治地位的测量理论。它对实得分数、真分数和测量误差关系进行了一系列的假定。

心理测验是对人的心理特质及其发展状况和水平的一种测验。前面讲过，由于人的心理特质的复杂性及内隐性，人们不可能像物理测量那样对其进行直接测度，只能通过给被试一组刺激（测试试题），然后根据被试对刺激做出的实际行为反应（回答测试试题情况）来间接推断他（她）的心理特质及其发展状况和水平。因此，定义一个用来刻画人的外显行为反应水平，且可据此来间接刻画人的心理特质及其发展状况和水平的特征量，就成为心理测验的首要条件。经典测量理论及其假设正是在这一思想基础上提出来的。

既然观察分数很难等于真分数，那二者之间是个什么关系呢？经典测量理论假定，观察分数（记为X）与真分数（T）之间是一种线性关系，并只相差一个随机误差（由随机因素例如考试中考生的情绪、考场的因素等所造成的实际成绩与其真正能力水平的差异，系统误差分数不引起观察分数的波动，被包含在真分数中），记之为E。

即：X = T + E 　(2. 1)

这就是经典测验理论（CCT）的数学模型，其实就是指个体的真实水平，在操作上是指为被试在无数个平行的测验上的得分的平均值（或期望值）。

根据这一模型，我们可以引伸出3个相关联的假设公理（Gulliksen，1950）：

① 若一个人的某种心理特质可以用平行的测验反复测量足够多次，则其测量分数的平均值会接近于真分数。

即：E(X)=T或E（E）=0

② 真分数和误差分数之间的相关为零。

即：ρ（T，E）=0

③各平行测验上的误差分数之间的相关为零。

即：ρ（E1，E2）=0

其中，第1条假设则在于说明E是个服从均值为零的正态分布的随机变量，也就是说，对于一组被试，其测验的误差的和为0，平均数也为0。第2、3条的假设意在说明E是个随机误差，只与偶然因素有关，而与真分数T的大小无关，测验误差并不随被试能力或心理特质水平的变化而出现有规律的变化，并不包括系统误差。

对经典测验理论（CCT）的这一数学模型及其假设公理，我们可以从以下3个方面来加以理解。首先，在问题的研究范围之内，反应个体某种心理特质水平的真分数是假定不会变的，测量的任务就是估计这一真分数的大小；

其次，观察分数被假定等于真分数与误差分数之和。即，假定观察分数与真分数之间是线性关系，而不是其他关系；

最后，测量误差是完全随机的，并服从均值为零的正态分布。它不仅独立于所测特质真分数，而且独立于所测特质以外的其他任何变量，这就保证了误差E中不含有系统误差成分。此外，各平行测验上误差分数间的相互独立也进一步保证了E的随机性，使得观察分数的均值可以稳定地趋于真分数。

值得注意的是，模型假设中所提到的平行测验是个重要的概念。经典测验理论（CCT）认为，如果两个题目不同的测验测量的是同一特质，并且题目形式、数量、难度、区分度以及测查等值团体后所得分数的分布（和标准差）都是一致的，则这两个测验就被称作是彼此平行的测验。

不过，用许多个彼此平行的测验反复测量同一个人的同一种心理特质的做法往往是很难实现的，因此，经典测验理论（CCT）的模型及假设只能是一种理论上的描述。然而，有了这一模型和假设之后，却能帮助我们解决测验中的许多实际问题。

事实上，我们在实施一个标准化测验时，并不是用许多平行测验来反复测查同一批被试，而是用一个测验来同时测查许多被试。由于每个人的误差都是随机的，且服从均值为零的正态分布，所以，当被试团体足够大时，团体内的各种随机误差会相互抵消，整个团体的观察分数的均值会趋近于该团体真分数的均值。这里，多个被试接受同一个测验相当于多个平行测验反复测查一个具有团体真分数均值水平的一个个体。因此经典测验理论（CCT）的理论模型和假设便派上了用场。

根据经典测量理论（CTT）模型和假设，我们很容易推导出如下关系：

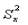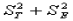= (2. 2)

即：在一次测量中，被试观察分数的方差等于其真分数方差与误差分数方差之和。

注意，公式（2.2）中只涉及到了随机误差的变异。系统误差的变异包含在真分数的变异之中。即：真分数还可以分成两部分：与测量目的有关变异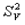（）和与测量目的的无关的变异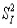（），即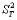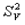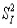：   = +  (2. 3)

于是 （2.2) 可以改写成：

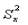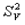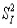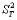=++   (2. 4)          

这就是说，一个测验中，一个团体的实测分数之间的变异性是由与测验目的有关的变异数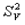（）、稳定的但出自无关来源的变异数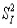（）和测量误差的变异数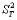（）所决定的。