当前位置:课程学习>>第四章>>学习内容>>文本学习>>知识点七
知识点七:单叶双曲面与双曲抛物面的直母线
我们在前面已经看到,柱面与锥面都可以由一族直线所构成,这种由一族直线所构成的曲面叫做直纹曲面,而构成曲面的那族直线叫做这个曲面的一族直母线。柱面与锥面都是直纹曲面。
我们又在第五节与第六节中看到单叶双曲面与双曲抛物面上都含有直线。下面我们来证明,这两类曲面不仅含有直线,而且可以由一族直线所构成,因而它们都是直纹曲面。
首先考察单叶双曲面
![]() (1)
(1)
其中![]() 为正的常数,把(1)改写为
为正的常数,把(1)改写为
![]()
或者
![]() (2)
(2)
现在引进不等于零的参数![]() ,并考察由上式得来的方程组
,并考察由上式得来的方程组
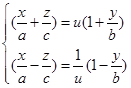 (3)
(3)
与两方程组
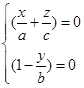 (4)
(4)
与
 (4')
(4')
方程组(4)与(4')实际上是(3)式中当参数![]() 和
和![]() 时的两种极限情形,显然不论
时的两种极限情形,显然不论![]() 取何值,(3)以及(4),(4')都表示直线,我们把(3),(4),(4')合起来组成的一族直线叫做
取何值,(3)以及(4),(4')都表示直线,我们把(3),(4),(4')合起来组成的一族直线叫做![]() 族直线。
族直线。
现在来证明由这族直线可以构成曲面(1),从而它是单叶双曲面(1)的一族直母线。
容易知道,![]() 族直线中的任何一条直线上的点都在曲面(1)上,这是因为
族直线中的任何一条直线上的点都在曲面(1)上,这是因为![]() 时,由两边相乘即得(1),所以(3)所表示的直线上的点都在曲面(1)上;而满足(4)与(4')的点显然满足(2),从而满足(1)因此直线(4)与(4')上的点也都在曲面(1)上。
时,由两边相乘即得(1),所以(3)所表示的直线上的点都在曲面(1)上;而满足(4)与(4')的点显然满足(2),从而满足(1)因此直线(4)与(4')上的点也都在曲面(1)上。
反过来,设![]() 是曲面(1)上的点,从而有
是曲面(1)上的点,从而有
![]() (5)
(5)
显然![]() 与
与![]() 不能同时为零,因此不失一般性,假设
不能同时为零,因此不失一般性,假设
![]()
如果![]() ,那么取
,那么取![]() 的值,使得
的值,使得
![]()
由(5)便得
![]()
所以点![]() 在直线(3)上。
在直线(3)上。
如果![]() ,那么由(5)知必有
,那么由(5)知必有![]() ,所以点
,所以点![]() 在直线(4)上。
在直线(4)上。
因此曲面(1)上的任一点![]() ,一定在
,一定在![]() 族直线中的某一条直线上。
族直线中的某一条直线上。
这样就证明了曲面(1)是由![]() 族直线所构成,因此单叶双曲面(1)是直纹曲面,而
族直线所构成,因此单叶双曲面(1)是直纹曲面,而![]() 族直线是单叶双曲面(1)的一族直母线,称为
族直线是单叶双曲面(1)的一族直母线,称为![]() 族直母线。
族直母线。
同样可以证明由直线
 (6)
(6)
(其中![]() 为不等于零的任意实数)与另两直线(相当于(6)中当
为不等于零的任意实数)与另两直线(相当于(6)中当![]() 和
和![]() 的情形)
的情形)
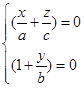 (7)
(7)
与
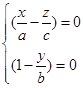 (8)
(8)
合在一起组成的直线族是单叶双曲面(1)的另一族直母线,我们称它为单叶双曲面(1)的![]() 族直母线。
族直母线。
图4-21表示了单叶双曲面上两族直母线的大概的分布情况。
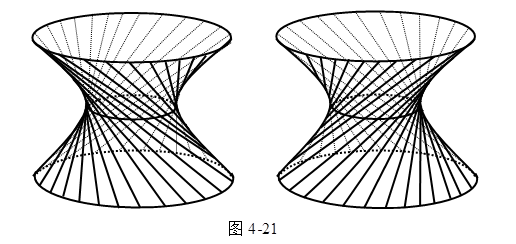
推论 对于单叶双曲面上的点,两族直母线中各有一条直母线通过这点。
为了避免取极限,我们常把单叶双曲面(1)的![]() 族直母线写成
族直母线写成
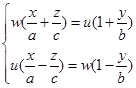 (4.7-1)
(4.7-1)
其中![]() 不同时为零。当
不同时为零。当![]() 时,各式除以
时,各式除以![]() ,(4.7-1)式就化为(3);当
,(4.7-1)式就化为(3);当![]() 时便化为(4);当
时便化为(4);当![]() 时便化为(4')。而
时便化为(4')。而![]() 族直母线写成
族直母线写成
 (4.7-2)
(4.7-2)
其中![]() 不同时为零。
不同时为零。
这里必须指出,(4.7-1)与(4.7-2)中的直线分别只依赖于![]() 与
与![]() 的值。
的值。
对于双曲抛物面
![]()
同样地可以证明它也有两族直母线(图4-22),
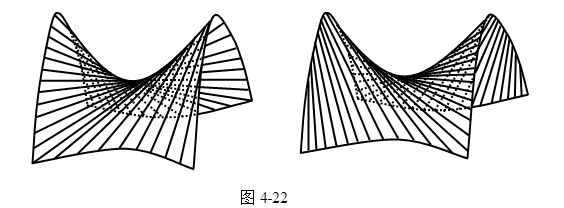
它们的方程分别是
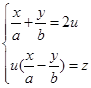 (4.7-3)
(4.7-3)
与
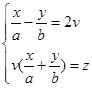 (4.7-4)
(4.7-4)
并且也有下面的推论:
推论 对于双曲抛物面上的点,两族直母线中各有一条直母线通过这一点。
单叶双曲面与双曲抛物面的直母线,在建筑上有着重要的应用,常常用它来构成建筑的骨架。
单叶双曲面与双曲抛物面的直母线还有下面的性质:
定理1 单叶双曲面上异族的任意两直母线必共面,而双曲抛物面上异族的任意两直母线必相交。
证 由(4.7-1)与(4.7-2)的四个方程的系数和常数项所组成的行列式为

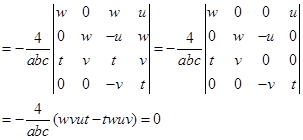
根据的第三章第八节的例3知道这两直线一定是共面的,所以单叶双曲面上异族的两直母线必共面。
同理可以判定双曲抛物面上的异族的两条直母线共面,又因为双曲抛物面上![]() 族直母线的方向数是
族直母线的方向数是![]()
,而![]() 族直母线的方向数是
族直母线的方向数是![]() ,从而这两条直母线是相交的直线。
,从而这两条直母线是相交的直线。
定理2 单叶双曲面或双曲抛物面上同族的任意两直母线总是异面直线,而且双曲抛物面同族的全体直母线平行于同一平面。
证明:这个定理前半部分的证明留给读者。
因为双曲抛物面上![]() 族直母线的方向数是
族直母线的方向数是![]() 线,故任意一条
线,故任意一条![]() 族直母线必平行于平面
族直母线必平行于平面![]()
![]() 族直母线的方向数是
族直母线的方向数是![]() ,从而任意一条
,从而任意一条![]() 族直母线必平行于平面
族直母线必平行于平面![]()
例 求过单叶双曲面![]() 上的点
上的点![]() 的直母线的方程。
的直母线的方程。
解 单叶双曲面![]() 的两族直母线方程是
的两族直母线方程是
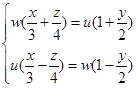 与
与 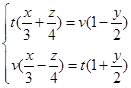
把点![]() 分别代入上面两组方程,求得
分别代入上面两组方程,求得
![]() 与
与 ![]()
代入直母线族方程,得过![]() 的两条直母线分别为
的两条直母线分别为
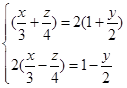 与
与 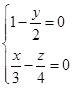
即:
![]() 与
与 ![]() 。
。
