|
第三章 数据的对比分析
第一节 数据对比分析的一般问题
有比较才有鉴别,数据对比分析即相对数分析是重要的统计分析方法。它是将两个有关的数据加以比较而得到的一个相对数,用以反映不同空间、不同时间的,也可以是不同性质的或事物内部各个组成部分的对比关系。计算各种相对数的基础指标是绝对数。
一、数据对比分析的基础指标
(一) 绝对数的概念
绝对数又称为总量指标,是社会经济现象总体在一定时间、地点、条件下的总规模、总水平或工作总量。它是最基本的统计指标,是计算相对指标和平均指标的基础。
绝对数既是社会经济现象总体的总规模、总水平或工作总量;也是社会经济现象总体在不同时间、地点、条件下数量增减变化的绝对离差。例如,山东与山西人口的差值,今年比去年国民生产总值的增减额等,也是绝对数。
统计总体有有限总体与无限总体之分,而只有有限总体才能计算其绝对数标。
(二)绝对数的作用
1 、绝对数是人们认识社会经济现象总体的起点。
反映现象总体的基本情况,首要的就是要掌握其在一定的时间、地点、条件下各方面的数量多少。
2 、绝对数是计算相对数和平均数的基础。
相对数和平均数一般都是由两个有关系的总量指标相对比产生的,它们是绝对数的派生指标。
3 、绝对数是实行宏观调控和微观管理的基本依据。
(三)绝对数的种类
1 、绝对数按其说明的内容不同可分为 { 1 总体单位总量 2 总体标志总量
总体单位总量用来表示总体中单位数的多少;
总体标志总量则表明现象总体单位某一数量标志值的总和。
总体单位总量和总体标志总量的地位不是一成不变的,而是随着研究目的和研究对象的不同发生变化。
2 、绝对数按反映的时间状态不同可分为 { 1 时期指标 2 时点指标
时期指标反映的是社会经济现象总体在一段时期内发展过程的累计总量;
时点指标则是用来表明社会经济现象总体在某一时刻(瞬间)上数量状况的总量
时期指标和时点指标的区别主要表现在以下三个方面:
( 1 )时期指标的大小直接受社会经济现象总体活动过程时间长短的制约,其数值大小与时间长短成正比。例如,对于某一特定总体有:年度指标大于季度指标大于月度指标。
时点指标的数值大小与时点的间隔长短就没有直接关系。不一定时点之间间隔越长,社会经济现象总体水平就越大。例如,某市人口年初为 4 00万,经过半年后可能有 4 10万,而到年底则可能只有 4 05万。
( 2 )作为时期指标,各个时期的数值是可以累加的,累加的结果可以说明一段较长的时间内社会经济现象总体所发生的总量。
时点指标的数值直接相加没有实际经济意义。
( 3 )时期指标的数值可以连续计数,它的每一个数据都可说明社会经济现象在这一时期内发生的总量,所以需要经常调查。
时点指标则只能间断计数,它的每个数据表明社会经济现象总体发展到某一时点上所达到的水平。通常采用一次性调查,每隔一段时间进行一次。
3 、绝对数根据其表现形式的不同可分为 { 1 实物量指标 2 价值量指标 3 劳动量指标
( 1 )实物量指标是反映事物使用价值的总量指标。与之相对应的实物单位是指根据事物的自然属性和特点而采用的计量单位。有自然单位、度量衡单位、标准实物单位三种。
自然单位是按照被研究现象的自然属性来度量其数量的计量单位。例如,人口以“人”为单位,牲畜以“头”为单位,鞋以 “双”为单位等等。
度量衡单位是按照统一的度量衡制度的规定来度量客观事物数量的一种计量单位。如,钢铁、粮食以公斤、吨为计量单位,棉布以米为计量单位,电机容量以千瓦为计量单位等等。
标准实物单位是按照统一折算的标准来度量被研究现象数量的一种计量单位。往往以复合单位表示。
( 2 )价值量指标是表明社会经济现象价值量的绝对数。它是用货币来度量社会财富和劳动成果总量的一种计量方法,其计量单位称为货币单位。具有广泛的综合性和较强的概括能力。
( 3 )劳动量指标是除实物指标和价值指标外,以劳动时间为单位计量劳动量或工作量的指标。一般以“工日”或“工时'为单位进行计量。
(四)绝对数的推算方法
| |
1 直接法 |
|
| 确定绝对数的方法 { |
( 1 )平衡关系推算法 |
| 2 推算法
{ ( 2 )因素关系推算法 |
| ( 3 )比例关系推算法 |
| |
( 4 )插值估算法
{ |
a 内插法 |
| b 线性插值法 |
| c 拉格朗日插值 |
( 1 ) 平衡关系推算法。
现象之间互相联系的关系,有很多可以表现为平衡关系,平衡关系推算法是一种利用社会经济现象之间存在一定的平衡关系,依据已知的指标来推算未知指标的方法。
( 2 ) 因素关系推算法。
社会经济现象一般可分解为若干个因素指标,因素之间相互联系有些可以表现为因果关系,即:现象的某项指标可以分解为若干影响因素指标,这些因素的指标的乘积等于该项指标的总量。利用因素间这种关系,根据已知资料推算未知的有关资料,就是因素关系推算法。
( 3 ) 比例关系推算法。
是根据已知的某一时期、某一地区或某一单位的某种指标与其相关指标的比例关系,来推算另一时期、另一地区或另一单位的指标;或者根据部分的资料利用其比例关系推算总体资料。比例关系推算法在统计中应用十分广泛。
( 4 )插值估算法。
插值估算法是根据若干已知项目的统计资料,来估算对应关系的未知项目的数值,或者根据变量数列和动态数列的若干已知对应数值,估算其数列中间所缺的未知对应数值。方法主要有内插法、线性插值法和拉格朗日插值法等。
A 、内插法。这种方法主要是根据平均发展速度,估算逐年缺少的数字资料。
B 、线性插值法。线性插值法是根据已知两项有关的对应关系资料,估计第三项对应的未知资料。它是应用两点式原理确定一个直线方程。其方程整理后得表示为:
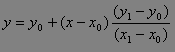
C 、拉格朗日插值法。当掌握的资料多于两项时,根据已知多项对应资料可用这种方法估计某项对应的未知数值。这种方法是线性插值多项式的推广。
二、相对数的概念
(一) 相对数的概念
相对数是应用对比的方法,来反映某些相关事物之间数量联系程度的综合指标。相对数是两个有联系的指标对比计算的比率。它从数量上反映事物在时间、空间、事物本身内部以及不同事物之间的联系程度和对比关系。
相对指标根据研究目的和任务不同,对比的基础不同,可以分为计划完成程度相对数、结构相对数、比例相对数、比较相对数、强度相对数、动态相对数等几种。
相对数的表现形式有 {1. 无名数 { a 计划完成程度相对数
b 结构相对数
c 比例相对数
d 比较相对数
e 动态相对数
2. 有名数—— 强度相对数 (具有平均的含义)
相对数的一般表现形式为无名数。无名数是一种抽象化的数值,常用倍数、系数、成数、百分数、千分数等表示。
(二)相对指标的作用
1 、相对数通过数量之间的对比,可以说明事物发生发展的程度、相互关联的程度和效益,因而有助于事物的鉴别。
2.相对数可以使某些利用总量指标无法直接对比的社会经济现象,找到可比的基础。
第二节 计划完成程度对比分析
一、计划完成程度相对数的意义及计算方法
计划完成程度相对指标是以社会经济现象在某时期内的实际完成数值与计划任务数值对比的结果,一般用百分数表示。其基本计算公式
计划完成程度相对指标 =( 实际完成数 / 计划完成数 ) ×100%
计划数是计算计划完成程度相对数的基数。基数的表现形式不一样,计划完成程度相对数在形式上也就不同。
1 、计划数为总量指标。可直接用实际水平和计划水平对比求得计划完成程度相对数。它一般适用于考核社会经济现象的规模或水平的计划完成情况。实践当中又分为两种情况,用两种方法来检查计划的完成情况:
( 1 )实际完成数与计划数是同一时期的指标。
计划完成程度相对数 = 实际水平 / 计划水平
( 2 )检查计划完成进度。此时计划期与实际完成的期限不一致,将计划期内某个时期的实际完成数值与整个计划期水平对比,可反映计划完成的进度。
2 、计划数为相对数。它一般是以前一期的实际数值为基础,规定计划比基数提高或降低的百分比。计算计划完成程度相对数时,应注意先将增减率变为完成率再进行计算。其计算公式为:
计划完成程度相对数 = 实际完成数( % ) / 计划数( % )
= ( 100% ± 实际提高或降低百分比) / ( 100% ± 计划提高或降低百分比)
3 、计划数为平均数。其计算公式为:计划完成程度相对数 = 实际平均数 / 计划平均数
例 1
计划完成相对数的计算
( 1 ) 计划数为绝对数:某企业某月计划产值为 600 万元,实际上完成 660 万元,则计划完成数为:
计划完成相对数 = 660/660 × 100 % = 110 %
超额的绝对数 = 660-600 = 60 (万元)
( 2 ) 计划数为相对数:某企业某种产品单位成本,计划规定比上期降低 7 %,实际降低 8.5 %,则计划完成相对数为:
计划完成相对数 = (100%-8.5%)/(100%-7%) = 98.39%
实际比计划多降低百分数 = 93 % -91.5 % = 1.5%
( 3 ) 计划数为平均数:某企业 2001 年第二季度某种产品的单位成本,计划规定为 80 元,实际为 76 元,则计划完成相对数为:
计划完成相对数 = 76/80 × 100 % = 95%
单位成本的节约额 = 80-76 = 4 (元)
二、长期计划执行情况的检查
(一)水平法。即:在长期计划中,只规定计划期末应该达到的水平(如,五年计划中规定最后一年应完成的产值、产量、商品销售额等指标等)。此时检查计划完成程度,应用下列公式:
计划完成程度 = 长期计划末年实际达到的水平 / 长期计划末年计划达到的水平
采用这种方法,只要有连续一年时间(如,第4年8月到第5年7月)实际完成的水平达到了计划末年水平,就算完成了五年计划,计算完成计划时间,则以提前4个月完成五年计划任务。
(二)累计法。即:在长期计划中,规定期间累计应完成的工作量或应达到的水平(如,新增生产能力、造林面积等等)。此时检查计划执行情况,应用下列公式:
计划完成程度 = 长期计划期间实际累计完成量 / 长期计划规定的累计数
采用这种方法,只要从长期计划期开始至某一时期止,所累计完成的数值达到了计划数值,就是完成了计划。如,从第1年到第4年10月份完成了5年的工作量,就是完成了五年计划,比计划时间提前1年零2个月。
长期计划执行情况检查:
( 1 )水平法:某厂 1996 ~ 2000 年计划规定最后一年( 2000 年)某产品应达到 400 万吨, 200 年实际产量 451 万吨。资料如下:
年份 |
1996 |
1997 |
1998 |
1999 |
2000 |
上半年 |
下半年 |
上半年 |
下半年 |
产量
(万吨) |
375 |
381 |
393 |
197 |
198 |
202 |
249 |
则有:计划完成相对数= 451/400 × 100 %= 112.75 %
自 1999 年 7 月~ 2000 年 6 月连续一年产量已达到 400 万吨,所以提前完成任务的时间为 6 个月。
( 2 )累计法:某地区“九五”计划基本建设投资总额为 40 亿元,执行如下:
年份 |
1996 |
1997 |
1998 |
1999 |
2000 |
上半年 |
下半年 |
上半年 |
下半年 |
投资额(亿元) |
11 |
9 |
12 |
8 |
6 |
5 |
7 |
可见,累计止 99 年上半年已达到 40 亿元,所以提前 18 个月完成任务。
第三节 数据的内部对比分析
数据的内部对比分析是指同一总体中,部分与总体之间,部分与部分之间的比率关系。具体有结构相对数和比例相对数两种形式。
一、结构相对数
社会经济现象的总体一般都是由许多不同的部分构成,并且按照不同的分类标准,可分为不同的部分,各个部分又都具有不同的性质和特征。研究总体时,了解其各个组成部分在总体中所占的地位和所起的作用有着重要的意义,这就需要利用结构相对数。
计算结构相对数,是先利用统计分组的方法,将总体分为不同性质的各个部分,然后以部分的数值与总体的数值对比。结构相对数一般用百分数来表示。其计算公式如下:
结构相对数 = 总体部分数值 / 总体全部数值× 100%
结构相对数的分子和分母,可以是总体单位数,也可以是总体标志数值。并且,由于结构相对指标是总体的部分数值与全部数值之比,每个部分所计算出的结果之和肯定为 100%。
∑总体内各部分比重 = 1 (或 100% )
在社会经济统计中,仅反映总体中某一特定部分占全体比重的结构相对指标即比率,应用也很广泛。比率可以用来说明事物的素质或者工作质量。
二、比例相对指标
在社会经济现象总体内部,各个组成部分之间存在着一定联系,往往具有一定的比例关系。为分析这种比例关系以及各部分之间的协调平衡情况,需要计算比例相对数。其计算公式如下:
比例相对数 = 总体中某一部分数值 / 总体中另一部分数值
例 4 比例相对数:某年某地出手婴儿中,男婴 1747 人,女婴 1663 人,
则有:新出生婴儿性别比例 =男婴数 / 女婴数 = 1742/1663
= 20 : 19
比例相对数通常用 n 比m或百分数来表示。用 n 比m的形式表示时,一般要求都是较简单的数值,以便让人一目了然。有时人们也习惯于把其中某部分数值定为 1 ,用 1 : m : n 的形式来描述总体各部分之间的比例关系。用这两种方法,由于数值相对比之后不一定都能得到整数或能够整除,因此常用其近似值来大概表示。
比例相对数也可以反映总体的结构,它所反映的比例关系是总体中结构性的比例。它同结构相对指标有着极密切的联系,其作用同结构相对指标相同,两者只是对比方式不同,侧重点各异。
第四节 数据的外部对比分析
数据的外部对比分析是指一个总体与另外一个同类或相联系的总体之间的比率关系。具体有比较相对数和强度相对数两种形式。
一、比较相对指标
比较相对数是反映某种社会经济现象在同一时间内不同空间条件下发展的不均衡程度。由于社会经济现象在不同的空间条件下,发展往往是不均衡的,要了解它们之间的差异程度,就需利用比较相对指标。其计算公式为:
比较相对数 = 某条件下的某类指标数值 / 另一条件下的同类指标数值
例 5 比较相对数:甲地区某年的国民生产总值 876 亿元,乙地区同年国民生产总值为 752 亿元,则有: 比价相对数: 876/752 = 1.1648 或 116.48 %
即甲地为乙地的 116.84 %或 1.1648 倍。
比较相对数也可以用于平均水平和标准水平的对比,用于先进与落后的比较。在一般情况下,比较相对指标的分子为对比单位,分母为典型单位。但是根据研究的目标选择出发点的不同,比较相对指标的分子和分母也可以对换。
二、 强度相对数
社会经济生活中,研究不同事物之间的数量对比关系,即由两个性质不同而有联系的总量指标对比得到的相对数,称强度相对数。其计算公式如下:
强度相对数 = 某一总量指标数值 / 另一性质不同而有联系的总量指标数值
例 6 强度相对数:人口密度为强度相对数。 2000 年我国人口密度为
129533 万人 /960 万平方公里= 135 人 / 平方公里
强度相对数用来表现社会经济现象的强度、密度和普遍程度,一般以复名数来表示。例如,人口密度指标(人/平方公里),人均国民收入指标(元/人)等,往往具有平均的含义。有些强度相对数还可以百分数或千分数来表示,如,人口自然增长率、商品流通费用率等。
强度相对数的用途十分广泛,如:
|
|
1 每元固定资金实现产值 |
| 2 百元产值占用流动资金 |
强度相对数 { |
2 反映生产条件和公共设施的配备情况
{ |
1 劳动力固定资产装备程度 |
| 2 劳动力的动力装备程度 |
|
3 反映国民经济和社会发展的基本情况
{ |
1 人口密度 |
|
2 每百人耐用消费品拥有量 |
|
3 人均国民收入 |
强度相对指标反映的是性质不同而又互相联系的总量指标的数值对比关系,因此,某些指标的分子和分母便可以相互转换,此时产生的强度相对指标就有了正逆之分。其中,数值大小与现象的发展程度或密度成正比例的,叫做正指标;反之,与现象的发展程度或密度成反比例的,则是逆指标。如:
商业网密度 = 商业机构数 / 人口数 (正指标)
商业点服务人口数 = 人口数 / 商业机构数 (逆指标) 第五节 数据的动态对比分析
动态相对数是某一指标在不同时间上的数值对比而得到的相对数。它说明同类事物在不同时间状态上的对比关系,对于分析社会经济现象的发展变化过程具有重要意义。
动态对比分析中,有两种时期概念:把作为比较标准的时期叫做基期,而把用来与基期对比的时期叫做报告期。
数据的动态对比分析方法有两种。即动态水平对比分析方法和动态速度对比分析方法两种。
一、动态绝对数对比分析方法
动态绝对数对比分析是以增减量指标为依据的。事物的增减量由报告期的数据减去基期数据而得到的一个差数,它是一个绝对数,这个绝对差数可以是正的,也可以是负的。显然,正的表示增加或提高的绝对量,负的表示减少或降低的绝对量。由于对比时采用了不同的基期数据,因此增减量又可分为“累计增减量”和“逐期增减量”两种。计算方法为:
1 、逐期增减量 = 报告期数据 — 报告期前一期的数据
2 、累计增减量 = 报告期数据 — 某一固定基期数据
3 、两种增减量之间存在着数量联系:
累计增减量 = 逐期增减量之和
二、动态相对数对比分析方法
动态相对数对比分析是以时间数列的速度指标为依据的。包括现象的发展速度和增减速度两种。
(一)发展速度比较
发展速度是将两个不同时期的同一现象的数据加以对比,抽象成为一个比率,用来表示某一现象在一段时间内的发展变化方向及其程度,通常用百分数表示。计算公式如下:
发展速度 = (报告期指标 / 基期指标)× 100%
在计算发展速度时由于所采用的基期不同具体由环比发展速度和定基发展速度两种对比分析方法。
1 、环比发展速度。
以报告前一期的数据为基期水平计算的发展速度称为环比发展速度。计算公式如下:
环比发展速度 = (报告期指标 / 报告期前一期指标)× 100%
2 、定基发展速度。
以某一固定时期数据为基期水平计算的发展速度称为定基发展速度。计算公式如下:
定基发展速度 = (报告期指标 / 某一固定时期指标)× 100%
3 、两种发展速度存在着数量联系:
定基发展速度 = 环比发展速度的连乘
(二) 增减速度的比较
增减速度是表明现象增减变化程度的相对指标,它可以根据增减量与基期水平对比取得,也可以将发展速度减“ 1 ”或 100% 求得。即:
增长速度 = 增减量 / 基期水平
= 发展速度 — 1 (或 100% )
增减速度和发展速度相似,由于所采用的基期不同,具体有环比增减速度和定基增减速度两种对比分析方法。
定基增减速度 = 定基发展速度 — 1 (或 100% )
= 累计增减量 / 最初水平
环比增减速度 = 环比发展速度 -1 (或 100% )
= 逐期增减量 / 前一期水平
在实际对比分析中,为了消除季节变动的影响,常以上年同季、同月发展水平作为对比基期计算年距速度指标。具体有:
年距发展速度 = 报告期水平 / 上一年同期水平
年距增减速度 = 年距发展速度 — 1 (或 100% )
例7、动态相对数:甲、乙企业总产值资料如下:
|
总产值(万元) |
第 3 期发展速度(%) |
第 3 期增减量(万元) |
1 |
2 |
3 |
环比 |
定基 |
逐期 |
累计 |
甲企业 |
10 |
12 |
15 |
125 |
150 |
3 |
5 |
乙企业 |
100 |
150 |
240 |
150 |
240 |
90 |
140 |
|
