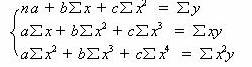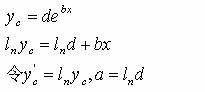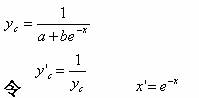第六章 相关分析和回归分析
    第一节 相关分析

    一、相关关系的概念
    所谓相关关系，从广义而言，乃是社会经济现象普遍存在的依存联系和制约关系，即客观现象之间互相关联的某种形式。
    社会经济现象之间的依存制约关系，具体表现出来的形态是多种多样的，但可区分为两种类型：
    1 、函数关系，又称确定性的关系，是指现象之间存在着确定的数量依存关系。
    2 、相关关系，又称不确定关系，是指现象之间确实存在着的，而关系数值不固定的相互依存关系。其特点为：
    (1) 相关关系是客观现象之间确实存在着的数量的相互依存关系。
    (2) 现象之间数量依存关系的具体关系值不是固定的。

    二、相关关系的种类

    三、相关关系的内容与步骤
    相关分析要反映和说明社会经济现象之间相互依存关系的数量关系，主要是了解现象间相互关系的密切程度和变化方向。进行相关分析先从定性分析开始，然后定量测定相关密切程度。
    （一）相关关系的一般判断
    （二）相关表
    定性分析的一般判断之后，把握着事物之间的相关关系，根据研究的具体目的，采集一系列相关数据，分别进行分组整理，罗列在一定表格内。依据观察单位和标志，编出相关表，从而初步了解相关关系的形式和程度。
    1 、简单相关表。
    将总体中各单位的原始资料或整理资料，按自变量和因变量的关系，由小而大列表排列，就形成了简单相关表。
    2 、分组相关表。
    分组相关表是将众多数据按某一标志进行分组而编制的。依据分组标志确定的多少有：单变量分组相关表和双变量分组相关表两种。
    （ 1 ）单变量分组相关表。是指在具有相关关系的两个变量中，只对一个变量进行分组，而另一个变量则不分组的分组相关表。
    （ 2 ）双变量分组相关表。对两个相关变量，都进行分组，计算出次数，列成相关表的形式，称之为双变量分组相关表。
    （三）相关图
    客观现象之间的相关关系资料，采用图像来显示，这种图像称之为相关图。
    相关图上的横坐标代表自变量 x ，纵坐标代表因变量 y 。把观察所取得的有关资料，依次以相关点标在图上，从相关点在图像上的分布及趋势，可以掌握变量之间的相关关系的状况。这种相关图，又称散点图。
    相关图的图形有如下几种表示：
    1 、强正相关。
    2 、弱正相关。
    3 、强负相关。
    4 、弱负相关。
    5 、非线性相关。
    （四）相关系数
    1 、相关系数的计算
    （ 1 ）积差法
    相关系数的基本计算公式是：
                                 
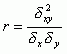
    其中：  r 是相关系数；
            δ_x 是自变量 x 数列的标准差；
            δ_y是因变量 y 数列的标准差；
            δ_xy 是两个变量数列的协方差。
    A 、对于未分组资料，相关系数的基本计算公式可以是：
                                 
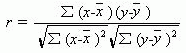
    简捷计算公式为：
                                 
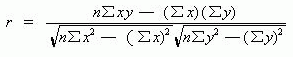
    B 、对于分组资料，就必须用各组的次数 f 加权计算相关系数。计算公式的基本表述是：
                                  
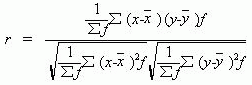
    可以简化为：
                                 
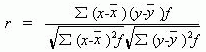
    2 、相关关系密切程度的划分。
                       0.3 以下——无相关
                       0.3 ～ 0.5 ——低度相关
    0 ≤ |r| ≤ 1 {    0.50 ～ 0.8 ——显著相关
                       0.8 以上——高度相关

   第二节  线性回归分析
   一、 回归分析的概念
    回归分析就是根据变量之间的主从或因果的回归关系，对变量之间的数量变化进行测定，建立一定数学模型，对因变量进行预测或估计的统计分析方法。

   二、简单线性回归分析的特点

   三、直线回归方程的确定
   直线回归方程一般表达式为： y_c=a+bx
   其中： y_c 表示对应于自变量 x 的因变量 y 的变动平均数（即估计值）。
   a 是直线的截距
   b 是直线的斜率，即回归系数。
   使用“最小二乘法”，即：参数 a 、 b 应满足∑ (y - y_c)²= 最小值 ，或者Σ (y - a - bx)²= 最小值。
   令 SSE= Σ (y - y_c)2= Σ (y - a - bx)²
   根据微分学中求极值的原理，分别求出ＳＳ E 对ａ和 b 的偏微分，并根据SSE是极小值的要求，使其偏微分等于零。从而计算整理出两个标准方程式：
                                         
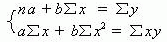
   依据上述两个标准方程，可以分别求解出如下两个参数值：
                                           
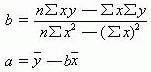
   如果已用积差法计算了相关数，有相应的资料，也可用如下方法求解：
                                            
   如运用分组相关表，同样可用前述方法建立直线回归方程和配合一条直线。与前述不同的是，在计算过程中，需用次数加权的方法。即，直线回归方程： y_c=a+bx 中的参数 a 和 b 的求解方程组是：
                                           
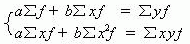
   因此，推导出求参数 a 、 b 值的公式为：
                                           

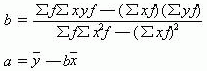
   四、估计标准误
   （一）估计标准误差的概念
   估计标准误差就是衡量 y 的实际值和估计值离差一般水平的分析指标。
   （二）估计标准误差的计算
   1、离差法。根据因变量实际值和估计值的离差，计算估计标准误差的方法，称之为离差计算法。其计算公式为：
                                           
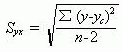
   公式中 n-2 是自由度。
   2、参数法。利用参数 a 、 b 的已知值，可以计算出估计标准误差，此方法谓之参数法。其计算公式的表述是：
                                         
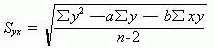
   （三）估计标准误差和相关系数的关系
   用公式表示为：
                                         

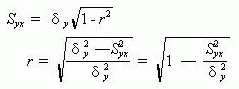
   五、多元线性回归方程
   （一）多元直线回归方程的建立
   多元线性回归方程的一般表述是： y_c = a + b₁x₁ + b₂x₂ + … + b_nx_n
   这里以二元回归方程为例说明。二元回归就是只用两个自变量来计算因变量的变化，它是多元回归的最简单的表现形式。其二元线性回归方程为：
   y_c = a + b₁x₁ + b₂x₂
   式中， y_c 为二元回归的估计值； a 为常数项；
   b₁ 与 b₂ 分别为 y 对 x₁ 和 x₂ 的回归系数。
   仍然运用最小平方法，分别求 x₁ 和 x₂ 的偏导，整理可以得到如下的三个标准方程式：
                                     
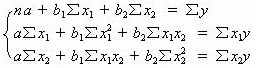
   即可根据此方程求得三个参数值。
   （二）多元回归的估计标准误差
   要说明多元回归方程推算结果的准确程度，就需运用多元回归估计标准误差分析指标。
   二元回归标准误差的基本公式是：
                                     
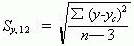
   S_y,12 代表二元回归估计标准误差。
   从基本公式推导出一个简捷计算公式：
                                
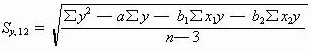
   （三）多元回归估计标准误差和复相关系数的关联
   二元回归的复相关系数与其回归估计标准差之间的关系用公式表述如下：
                                     

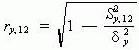
   第三节 非线性回归分析
   一、非线性回归分析的意义
   非线性相关和回归分析一般是通过变量的变换将非线性模型线性化，再按照线性回归分析的方法处理。

   二、非线性回归方程
   （一）指数曲线方程
                 
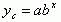
   改变成对数模式：
               
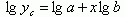
   令
              
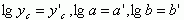
   则有线性方程：
              
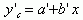
   求解 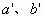值后，引入替代式，可找出曲线方程的参数 a 与 b 的值。
   （二）双曲线方程
   当因变量随着自变量而增加，最初增加很快，以后渐趋减慢而后呈现平稳之势，这种相关关系，可以采用双曲线配合，建立双曲线回归方程，进行回归分析。
   双曲线回归方程式是：
                 
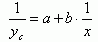
               令
                 
   则原方程变换为：
                 
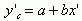
   （三）抛物线方程
                 
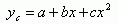
   公式中的 a 、 b 、 c 是待定参数。
   由于 x 和 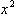具有明显的共线性，所以不能如上两种形式那样变换变量，而要用“最小平方法”。
   令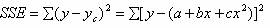
   欲使 SSE 取最小值，需求 SSE 的偏微分，并令其等于零，从而整理得如下三个标准方程组：
                                
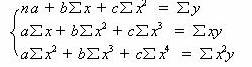
   求解此方程组，可得到唯一的一组解，就是抛物线方程式的参数 的值。
   （四）其它曲线方程
   研究社会经济生活现象的非线性相关与回归问题，除了前述三种较常运用外，有时还可运用幂函数曲线、公伯兹曲线和罗杰斯提曲线等。这些曲线方程简列如下：
   1、 幂函数曲线方程。
                                      
   则改变为线性方程，
  
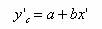
   2、公伯兹 (Gompertz) 曲线方程。
                             
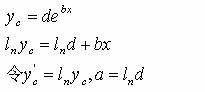
   则改变为线性方程
  
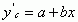
   3、罗杰斯提（ Logistic ）曲线方程。
                             
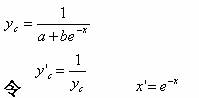
   则改变为线性方程
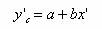