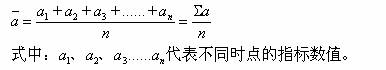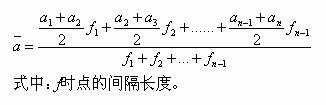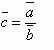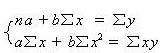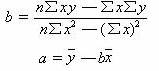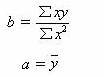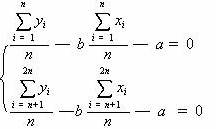|
第七章 时间数列
第一节 时间数列的概念和种类
一、时间数列的概念
统计学把各个时期的统计资料按时间先后顺序加以排列而组成的数列称为时间数列或动态数列。
时间数列一般用表格的形式表现,它有两个基本要素构成:
一是现象所属的时间;
二是反映现象特征的各项指标数值。
二、时间数列的种类
时间数列按所列统计指标的性质不同,可分为:
(一)绝对数时间数列
由总量指标组成的时间数列称为绝对数时间数列,它反映社会经济现象在不同时期达到的总规模、总水平以及发展过程和变化趋势。
绝对数时间数列又有时期数列和时点数列之分。
1 、时期数列
时期数列的各项数值反映某一阶段内社会经济现象的总量。
2 、时点数列
时点数列的各项数值反映某种社会经济现象在一定时点上的规模或水平。
3 、时期数列和时点数列的特点及区别
(二)相对数时间数列
由相对指标构成的时间数列称为相对数时间数列,它反映社会经济现象不同时期的比例、结构、强度等对比关系的发展变化过程及其特征。
(三)平均数时间数列
由平均指标构成的时间数列称为平均数时间数列,它反映社会经济现象不同时期一般水平的发展变化过程及其特征。
三、时间数列的编制原则
第二节 时间数列的水平指标
时间数列的水平指标有发展水平、增长量、平均发展水平和平均增长量。
一、发展水平和增长量
(一)发展水平
发展水平一般是指时间数列的总量指标,用 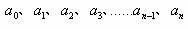 表示。 表示。
(二)增长量
增长量是两个不同时期发展水平对比的绝对差额,它用来说明某种现象在一定时期内增长或减少的绝对数量。增长量的计算公式为:
增长量 = 报告期水平—基期水平
由于采用的对比基期不同,增长量可分为:
1 、逐期增长量
逐期增长量说明本期比上期增长或减少的绝对量,用符号表示为:
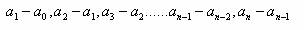
2 、累积增长量
累积增长量说明本期比某一固定时期增长或减少的绝对量,它可以说明现象在某一段时间范围内总共增长的绝对量,用符号表示为:
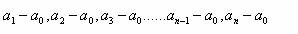
逐期增长量和累积增长量的数学关系是:
( 1 )一定时期内的累积增长量等于该段时期内相应的各个逐期增长量之和,用符号表示为:
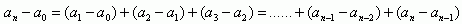
( 2 )两个相邻的累积增长量之差等于相应的逐期增长量,用符号表示为:
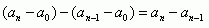
3 、年距增长量
年距增长量表明报告期水平较上年同期(季、月、日)水平的增长或减少的绝对量,它能消除季节变动的影响。
二、平均发展水平与平均增长量
(一)平均发展水平
将不同时期的发展水平加以平均而得的平均数叫平均发展水平,亦称序时平均数或动态平均数。由于反映事物发展的时间数列有绝对数时间数列、相对数时间数列和平均数时间数列,它们计算序时平均数的方法也有所不同。
1 、绝对数时间数列计算序时平均数。因为绝对数时间数列分时期数列和时点数列两种,它们具有不同的特点,所以计算序时平均数的方法也有所不同。
由时期数列计算序时平均数
(1) 由于时期数列中各项指标数值可以直接相加,所以采用简单算术平均法计算,即:

(2) 由时点数列计算序时平均数
由于时点数列都是由一系列某一时点上瞬间资料编制的,按其资料登记是否连续分为:连续时点数列和间断时点数列两种,其计算方法也不一样。
①连续时点数列计算序时平均数
A 、间隔相等的连续时点数列可以像时期数列那样运用简单算术平均法进行计算,其计算公式为:
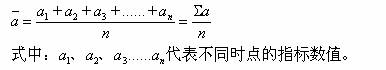
B 、间隔不等的连续时点数列是以各时点之间的间隔期为权数,用加权平均法来计算序时平均数的,其计算公式为:

②间断时点数列计算序时平均数
A、对于间隔相等的间断时点数列,需先计算各相邻两期发展水平的平均数,然后将这些平均数再用简单平均法求序时平均数,这种方法也叫首末折半法。计算公式为:

B 、对于间隔不相等的间断时点数列,要以各时点之间的间隔长度为权术, 将各相应的时点的平均数加权来计算序时平均数。计算公式为:
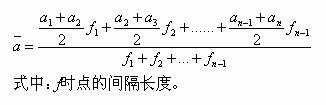
2 、相对数时间数列计算序时平均数
因为相对数时间数列是由两个有密切联系的绝对数时间数列相应项对比而形成的,而各个相对数不能直接相加。所以由相对数时间数列计算序时平均数,必须将构成相对数时间数列的两个绝对数时间数列,即分子和分母的序时平均数进行对比。其基本计算公式为:

3 、平均数时间数列计算序时平均数
由一般平均数时间数列计算序时平均数时,也不能直接通过数列中的平均指标值简单平均求得,必须先计算分子、分母的序时平均数后,再进行对比求得。其基本计算公式亦为:
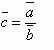
(二)平均增长量平均增长量是说明某种现象在一定时期内每期平均增加或减少的数量。它是逐期增减量的平均数。

第三节 时间数列的速度指标
时间数列的速度指标有发展速度、增长速度、平均发展速度和平均增长速度。
一、发展速度和增长速度
发展速度和增长速度都是动态相对数,它们用来反映某种现象在一定时期内的发展方向和变化速度。
发展速度和增长速度用下式表示:

在计算发展速度和增长速度之前,应根据研究对象和研究目的,选定恰当的对比基期。常用的对比基期有三种:
1、以相邻的上一期水平为基期水平,形成环比发展速度和环比增长速度。

2、以某一固定时期水平为基期水平,形成定基发展速度和定基增长速度。

环比发展速度和定基发展速度之间存联系是:
(1) 一定时期内的定基发展速度等于该时期内各个环比发展速度的连乘积,即:

(2) 两个相邻时期定基发展速度之商等于相应的环比发展速度,即
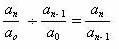
3 、以去年同季、同月发展水平作为对比基期,形成年距发展速度和年距增长速度。

二、平均发展速度和平均增长速度
平均发展速度是根据时间数列中的各个环比发展速度计算的序时平均数。应采用几何平均数的方法。
几何平均数( Geometric Mean )也是常用的平均数之一,其基本算式为:
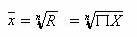
式中: R 代表某个时期内现象发展的总速度(即定基发展速度);
X 代表各个环比发展速度;
n 代表环比发展速度的项数;
Л代表连乘符号。
由于环比发展速度的连乘积等于定基发展速度,所以,平均发展速度又可等于定基发展速度的 n 次方根,用公式表示为:
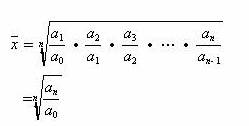
平均增长速度,又称平均递增率,由平均发展速度减 1 或 100% 求得。
三、增长 1% 的绝对值
这是一个由相对数和绝对数相结合运用的指标。

第四节 长期趋势的测定
一、长期趋势的概念和测定的意义
时间数列由四个因素组成:长期趋势( T ),季节变动( S ),循环波动( C ),不规则波动( I )。
长期趋势是指社会经济现象在较长时期内表现出持续向上或向下发展的变化趋势。
二、移动平均法
移动平均法是把时间数列的各期指标数值,根据确定的时间长度,用逐项移动的方法计算序时平均数,这样计算出来的是一个消除了偶然因素影响的新的时间数列。
采用三项移动平均的计算公式为:
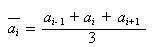
采用五项移动平均的计算公式为:
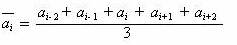
移动平均采用奇数项移动能一次对准被移动数据的中间位置,比较方便。如果采用偶数项移动平均,一次移动平均后的数值将置于居中的两项数值之间。
三 、指数平滑法
指数平滑法是对不同时期的观察值用递减加权的方法修匀时间数列的波动,从而对现象的发展趋势进行预测的方法。
一次指数平滑法的基本公式如下:
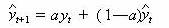
式中: y 表示实际观察值;
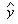 表示预测值; 表示预测值;
t 表示不同时期( t 可理解为本期, t +1 为下一期或预测期, t — 1 为上一期);
α表示平滑系数或比重权数( 0 <α< 1 )。
四、最小平方法
最小平方法又称最小二乘法,是分析和预测现象长期趋势常用的方法之一。它的基本思想是:要通过对原始数列的数学处理,拟合一条比较理想的趋势线,使原数列各数据点与趋势线垂直距离的离差平方和为最小。
根据最小平方法的要求,建立直线趋势方程:yc=a+bx
其中: yc 表示时间数列 y 的理论趋势值;
x 表示时间序号;
a 和 b 为直线方程的两个待定参数, a 是直线的截距 b 是直线的斜率。
由于“最小二乘法”,参数 a 、 b 应满足Σ( y — yc ) 2= 最小值,或者Σ( y — a — bx ) 2 =最小值,则令 Q= Σ( y — yc ) 2= Σ( y — a — bx ) 2
要使其等于最小值,则分别求出 Q 对a和 b 的偏微分,并使其偏微分等于零。从而计算整理出两个标准方程式:
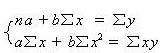
依据上述两个标准方程,可以分别求解出如下两个参数值:
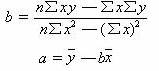
由于 x 的数值是人们按一定顺序排列确定的,为了计算方便,我们可以假设时间数列序号 x 满足Σ x = 0 ,则可简化求a、b的计算公式为:
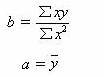
当时间数列为奇数项时,可把时间数列最中间的一项编序号为 0 ,以上各项为 -1 、 -2 、 -3 …顺序编排,以下各项为 1 、 2 、 3 …编排。
当时间数列为偶数项时,可把时间数列居中的两项分别编为 -1 和 1 ,以上各项按 -3 、 -5 、 -7 …编排,以下各项按 3 、 5 、 7 …编排,即各时间序号以间隔 2 的顺序编排。
五、半数平均法
半数平均法,也称平均法,是分析和预测现象长期趋势的方法之一。这种方法是运用数学上两点确定一条直线的原理而建立的
按照半数平均法的要求,建立直线趋势方程为: yc = a + bx
式中: yc 表示时间数列中y估计趋势值;
x 表示时间顺序;
a和 b 为直线方程的两个待定参数。
半数平均法要求,趋势直线应该满足Σ(y— yc) = 0 ,即指实际值与估计趋势值之间离差总和等于零。
将 yc = a + bx 代入Σ(y— yc ) = 0 ,整理可得:
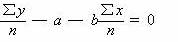
式中: 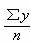 和 和 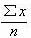 是两个平均数。 是两个平均数。
将原时间数列分成相等的两部分,若实际的时间数列资料是奇数项,则消去最早的一项数据,使数据项为 2n 个;然后,按两部分平均数,建立一组联立方程式:
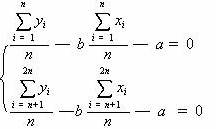
求解联立方程,即可求得 a 与 b 参数的值。
第五节 季节变动的测定
一、季节变动的概念和测定的意义
社会经济现象受自然因素和社会因素的影响,在一年内随着时间变化而引起比较有规律的周期性变化,称为季节变动。
二、同期平均法
同期平均法是把 3 年或 3 年以上同月或同季的资料按年排列,计算出各月或各季的同期平均数,并与月(季)总平均数进行对比,得出的相对数,即为反映季节变动的测定指标——季节比率。
具体测定步骤如下:
1 、分别求出各年同月(或同季)资料的简单算术平均数。
2 、求出各月的月总平均数(或季总平均数)。
3 、用各年同月(同季)平均数分别除以月(季)总平均数,得出 12 个月(或 4 季)的百分数,这些百分数就是季节比率。
4 、若季节比率误差太大,则用调整系数调整。
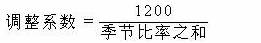
调整后的季节比率 = 原季节比率 ×调整系数
5 、把各月(季)季节比率绘成季节变动曲线图,可以更直观地显示出季节的变动趋势。
三、移动平均趋势剔除法
这是利用移动平均法来剔除长期趋势的影响后,再确定季节变动的方法。
12 个月移动平均法的具体计算步骤如下:
1 、据各年月资料以 12 个月移动平均求得长期趋势值 T 。
2 、计算出各月的季节比率,以消除长期趋势(或循环变动)对季节变动的影响。
根据各因素的乘法公式进行等式变换,可得:
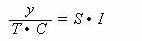
若没有循环变动,则公式变为: 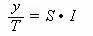
所以将各月的实际值 y 除以相应的各月长期趋势值(或再除以循环变动值),剩下季节变动与不规则变动,然后采用同月简单平均的方法消除不规则变动,即得季节比率。
3 、将求得的季节比率重新按月编排,再计算各年同月的季节比率的简单算术平均数,从而得到消除了不规则变动因素的季节比率。
4 、若各月季节比率合计数不等于 1200% ,应用调整系数予以调整。
|