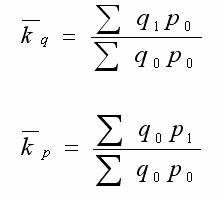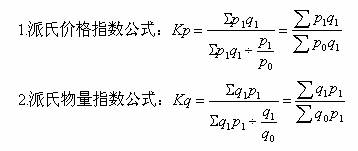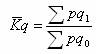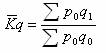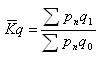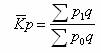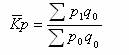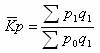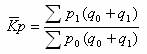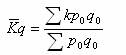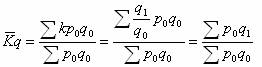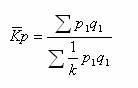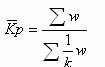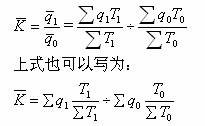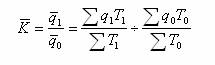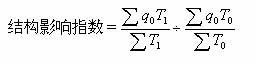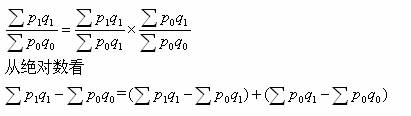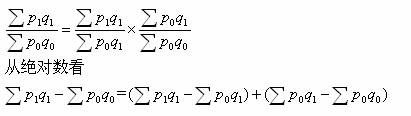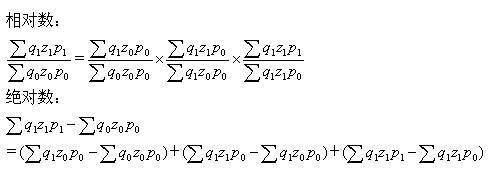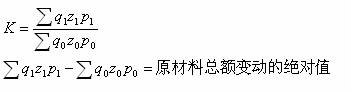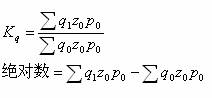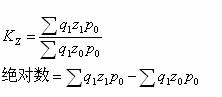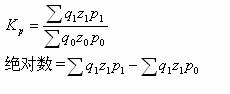第八章 统计指数
   第一节 统计指数的概念和类型

   一、指数的概念
   指数是一种表明社会经济现象总体数量变动的特殊相对数，它既能反映简单、个别社会经济现象数量变动的方向和程度，也能反映复杂、总体社会经济现象数量变动的方向和程度。
   指数的含义有广义和狭义之分：
   广义的指数——泛指所有社会经济现象数量对比的相对数，包括不同时间、不同空间的同类经济现象数量指标以及实际完成指标与计划完成指标对比而形成的各种相对数。
   狭义的指数——指反映总体社会经济现象中，不能直接加总和不能直接对比的多种不同事物在数量上总变动的一种相对数。统计中通常编制的指数，是就狭义的指数而言。
   指数起源于物价指数，物价指数的公式为：
                                             
   由于上述计算公式均是假定各种商品在市场份额相等，而这个假设与实际是不相符的，于是产生了考虑各种商品在市场上所占份额的加权指数。
   根据所使用的权数不同，可将指数分为两类。
   一类是拉氏指数。特点是用基期指标值作为指数计算中的权数
                                            
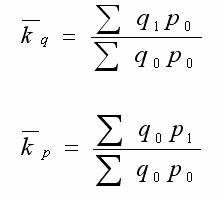
   另一类是派氏指数。它用报告期指标值代替拉氏指数计算过程中的基期指标值。公式如下：
                                 

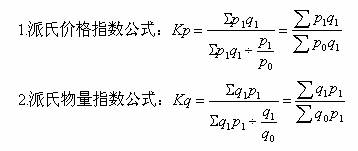
   二、指数的作用
   （一）综合反映社会经济现象总体数量变动方向和变动程度 。
   （二）分析和测定复杂社会经济现象中各因素对总量变动的影响方向和影响程度。
   （三）用来研究社会经济现象的长期变动趋势。
   （四）用来对社会经济现象进行综合评价和测定。

   三、指数的类型
                     

   第二节 综合指数

   一、综合指数的意义和特点
   （一）综合指数的意义
   （二）综合指数的特点
   1 ．先综合后对比。
   2 、把总量指标中的同度量因素加以固定，以测定所要研究的因素，即指数化指标的变动程度。
   3 、综合指数的分子、分母在所研究对象的范围上必须保持一致，所反映的现象变动程度应是所综合的资料范围内该现象的变动程度。

   二、综合指数编制的原则和方法
   构成现象总体的因素，大体可分为数量因素和质量因素。所以，综合指数也就分为数量指标综合指数和质量指标综合指数。
   （一）数量指标综合指数
   数量指标综合指数——是说明数量指标变动情况，即总体规模变动情况的比较指标。如，工业产品生产量指数，其一般公式为：
                                             
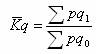
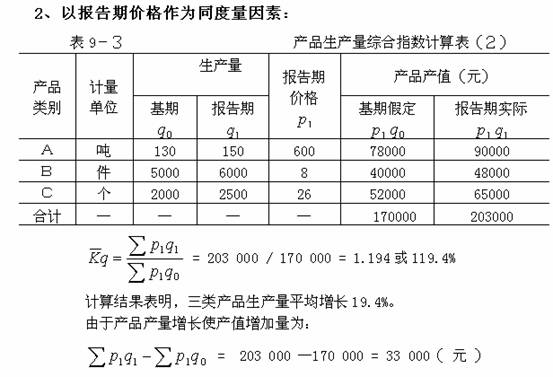
   1、以基期价格作为同度量因素，其公式为：
                                             
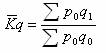
   这个公式被称为拉氏物量指数公式，其计算结果的经济意义是：假定在基期价格水平的情况下；产品生产量的综合变动方向和程度。分子与分母的差额 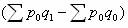，说明由于产品生产量变动对产值绝对数的影响程度。
   2 、以报告期价格作为同度量因素，其公式为：
                                             
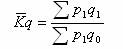
   这个公式被称为派氏物量指数公式，其计算结果的经济意义是：假定在报告期价格水平的情况下，产品生产量的综合变动方向和程度。分子与分母相减的差额 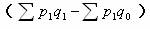，说明由于生产量变动对产值绝对数的影响程度。
   3、以某一固定时期的不变价格作为同度量因素，其公式为：
                                             

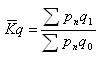
   < 例如 >
                     
                      
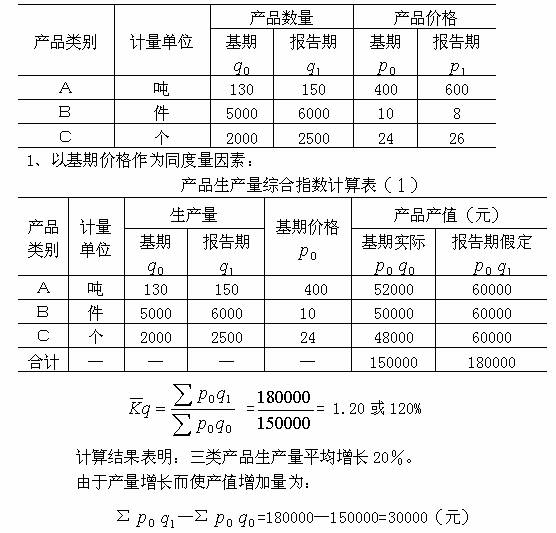
   （二）质量指标综合指数
   质量指标综合指数——是说明质量指标变动方向和程度的指数。它是反映总体内质量指标变动情况的比较指标。如商品价格指数，其公式为：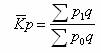                                                

   1、以商品销售作为同度量因素，其公式为：
                                              
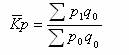
   这个公式又叫拉氏质量指数公式。计算结果的经济意义是：假定在基期数量指标不变的情况下，质量指标的综合变动方向和程度。分子与分母的差额 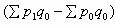，说明由于价格水平变动对总销售额绝对数的影响程度。
   2、以报告期商品销售量为同度量因素，其公式为：
                                                
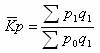
   这个公式又叫派氏质量指数公式。
   计算结果的经济意义是：分子与分母的差额 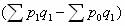，说明由于价格水平变动对总销售额绝对数的影响程度。
   3、以报告期和基期商品销售量之和为同度量因素，其公式为：
                                             
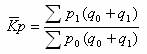
   在国外，将这种公式叫马歇尔—埃奇沃思公式。

   三、综合指数的同度量因素的选择
    < 例如 >二、质量指标综合指数（以上表资料为例）
                              
   同度量因素——是指在计算综合指数时，解决总体中各个个体不能直接相加的媒介因素，其作用就是使不能直接相加的指标过渡到能够相加的指标。
   选择同度量因素的指标的主要原则是：要根据现象之间的经济联系，用与指数化指标具有相互联系的指标作为同度量因素。关于同度量因素的时期确定，主要以下几个方面：。
   其一，要从指数本身的经济意义考虑。
   其二，从指数体系的要求考虑
   其三，从实际应用和是否便于取得资料方面考虑
   在国内，一般情况是：编制质量指标指数，采用报告期数量指标为同度量因素；编制数量指标指数，采用基期质量指标为同度量因素。

   第三节 平均数指数

   一、平均数指数的意义
   平均数指数——是总指数的另一种计算形式。它是以个体指数为基础，采用加权形式编制总指数，以测定总体现象的平均变动程度。

   二、平均数指数的编制方法
   平均数指数有两种基本形式：一是加权算术平均数指数；二是加权调和平均数指数。由于所使用的权数不同，每种形式又包括综合指数变形计算形式和固定权数计算形式。
   （一）综合指数变形形式的平均数指数
   1、加权算术平均数指数。它一般在编制数量指标指数时运用。只要掌握了个体数量指数以及综合指数的分母（基期的实际数）数值时即可。其公式为：
                                                
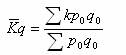
   平均指数与综合指数之间存在着变形关系：
                                    
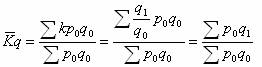
   若使用 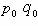以外的任何其它权数，则不存在上述这种变形关系。
   < 例如 >
   2、加权调和平均数指数。它一般适用于编制质量指标指数。其公式为：
                                                
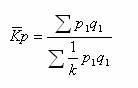
   综合指数与调和平均指数之间存在着变形关系。即：
                                    
   在计算总指数时，是直接用综合指数计算还是用其变形形式加权平均指数来计算，要根据所掌握的资料而定。
   < 例如>
   （二）固定权数形式计算的平均指数
   1、用固定权数计算加权算术平均指数。固定权数是指用某一时期，经过调整后的权数资料，以比重的形式固定下来作为权数，通常用Ｗ表示。
   固定权数计算的算术加权平均指数中的Ｗ，与 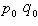的口径、范围可能不一致，时期也可能不一致。
   固定权数算术加权平均数指数公式为：
                                         
   < 例如 >
   2、用固定权数计算加权调和平均指数。以Ｗ代表固定权数，加权调和平均数指数公式为：
                                                   
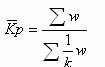
   这种公式在实际工作中较少运用。

   三、平均数指数的特点
   与综合指数相比，平均数指数有以下特点：
   1 ．平均数指数解决了综合指数编制中全面资料不易取得的问题。
   2 ．平均数指数的权数可以采用多种方法，例如综合指标或比重形式。

   四、固定加权平均数指数的应用
   平均指数由于具有以上两个综合指数无法替代的优点，因此具有十分广泛的实用价值。尤其是固定权数加权算术平均数指数应用更为广泛。在采用固定权数加权算术平均数指数时，应解决好以下几个问题：
   （一）代表品的选择
   应遵循三条基本原则：
   1、代表品要有充分的代表性。
   2、选择那些对国计民生影响较大的品种。
   3、选择经济寿命比较长、有发展前途的品种，力求避免选择那些行将淘汰的品种。
   （二）权数的编制
   加权算术平均数指数的权数编制，涉及到权数的内容、编制权数的方法等问题。
   编制权数的方法主要有三种，即直接权数、附加权数和分层分摊权数。以销售额指标作权数为例分别加以说明。
   直接权数——是以全部代表品的销售额为 100% ，然后求各代表品的销售额在全部代表品销售额中所占的比重，这个比重，就是代表品的权数。
   附加权数——是指附加在每一代表品上的权数，这里不仅有该品种的权数，另外还有那些由该代表品在指数中所代表的那一部分品种的权数。
   分层分摊权数——是指将非代表品的销售额分层分摊到代表品上。假定指数分为大类、中类、小类、产品四层，其具体计算步骤为：
   第一层计算代表大类权数。求出各代表大类的销售额占全部代表大类销售额的比重，此比重即为大类权数。
   第二层计算代表中类权数。从代表大类中选出代表中类产品，求出各代表中类的销售额占全部代表中类销售额合计的比重，再用这个比重乘以该大类权数，其积即为各代表中类权数。
   第三层计算各代表小类权数。从代表中类选出代表小类产品，求出各代表小类的销售额占全部代表小类销售额合计的比重，再用这个比重乘以该中类权数，其积即为各代表小类权数。
   第四层计算各代表产品权数。从代表小类中选出代表品，求出各代表品的销售额占小类中全部代表品销售额合计的比重，再用这个比重乘以小类权数，其积即为各代表品权数。

   第四节 平均指标指数因素分析

   一、平均指标指数的含义
   平均指标指数——是同一经济内容的两个不同时期的平均指标数值之比，它是对平均指标的变动情况进行分析的一种方法。其一般公式为：
                                       
   常见的平均指标指数有：劳动生产率指数、平均工资指数、平均单位成本指数等。下面以劳动生产率指数为例，介绍平均指标指数的基本原理和分析方法。
   劳动生产率指数的公式如下：
                                          
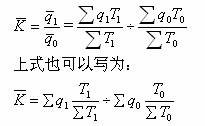
   显而易见，劳动生产率指数反映两个因素变动的影响，即各种工人劳动生产率变动的影响和各组工人人数在全部工人总数中所占比重变动的影响。这是因为加权算术平均数本身包括标志值和权数两个因素，所以平均指标指数所反映的变动程度，也包括两个因素的影响，即不仅受所平均的经济指标变动的影响，而且还受所研究总体内部单位数结构变动的影响。

   二、平均指标指数的因素分析
   平均指标指数变动既包括标志值，也包括权数构成的变动。下面我们将通过计算三种指数形式来分析。
   （一）可变构成指数
   可变构成指数——是指现象总体的变动由各组平均水平和总体结构变动两个因素相互作用的结果的指数。
   其公式为：
                                         
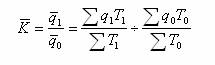
   （二）固定构成指数
   固定构成指数——是指将总体结构假定在报告期条件下，计算出来的指数。其公式为：
                                       
   （三）结构影响指数
   结构影响指数——是指将各单位水平假定基期条件下，计算出来的指数。其公式为：
                                       
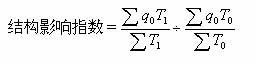
   （四）上述三个指数之间的联系
   可变构成指数、固定结构指数和结构影响指数三者之间具有一定的内在联系，形成一个指数体系。即：
                             
   < 例如 >

   第五节 指数体系和指数数列

   一、指数体系和因素分析
   （一）指数体系的含义和作用
   我们把那些经济上有联系、在数量上保持一定关系的若干指数形成的整体，称作指数体系。组成指数体系的指数必须满足这样两个条件，即：各因素指数的乘积应等于总变动指数；各因素指数分子分母差额的总和，应等于总量指标指数实际发生的总差额。
   根据因素指数所采用的同度量因素的不同时期，通常组成两套指数体系。
   1、 质量指数将同度量因素固定在报告期，而数量指数则将同度量因素固定在基期，形成的指数体系为：
                           
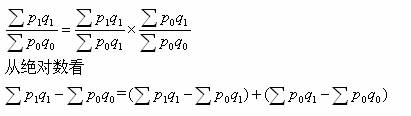
   2、质量指数将同度量因素固定在基期，而数量指数则将同度量因素固定在报告期，形成的指数体系为：
                           
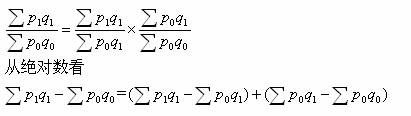
   这两套指数体系在实际工作中要根据实际情况而灵活选用。
   指数体系的主要作用表现在两个方面，即：根据指数体系中各指数间的相互联系，从任意两个已知的指数推算第三个指数；根据指数体系中因素指数与总指数的关系，分析各因素变动对总变动的影响方向和程度，以及影响的绝对值。
   （二）指数体系的分析方法
   指数体系是进行因素分析的基本依据。进行因素分析按包含因素的多少，可以是两因素的分析，也可以是两因素以上的因素分析；按分析指标的种类，可以是总量指标的因素分析，也可以是平均指标的因素分析。
   1、总量指标的两个因素分析。它分析的对象是由两个因素组成的总量指标。分析的目的是分别测定这两个因素的变动对总量变动的影响程度和影响方向。以产品产值总量为例：
   指数体系用公式表示为：
                     
   < 例如 >
   2、总量指标的多因素分析。
   （ 1 ）要对各个因素进行合理排列。
   排列的原则是：
   ①先数量指标，后质量指标；
   ②先实物指标，后价值指标；
   ③相邻的指标具有经济意义。
   （ 2 ） 分析某一因素变动对总变动的影响时。要固定其它因素。当测定数量因素变动时，将作为同度量因素的质量因素固定在基期；反之，当测定质量因素变动时，将作为同度量因素的数量因素固定在报告期。这是同度量因素选择的原则。
   在多因素分析的指数体系中，总变动指数与各因素指数的乘积是相等的；实际发生的总变动额与各因素变动额的和也是相等的。这一基本原理通常可用来检验实际工作的正确性。用公式表示为：
                          
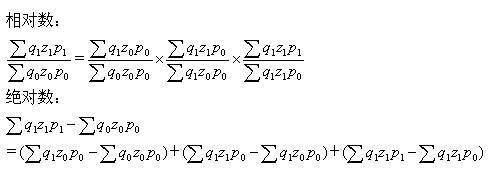
   下面以原材料总额因素分析为例：
   原料总额 = 产量×原材料单耗×原材料单价
   （ 1 ）原材料总额指数
                                    
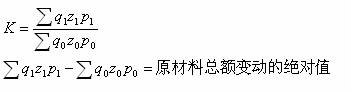
   （ 2 ）各因素分析
    ① 产量指数
                                          
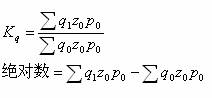
    ② 原材料单耗指数
                                          
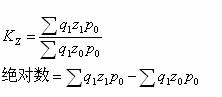
   ③ 原材料单价指数
                                          
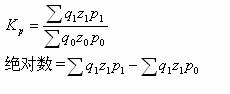
   （ 3 ）综合因素分析

   二、指数数列
   指数数列，就是将各个时期的一系列指数，按照时间先后顺序排列起来所形成的数列。可见，指数数列也是一种时间数列。其特点在于数列中所排列的各项指标都是指数，而不是一般的综合指标。
   （一）个体指数数列和总指数数列
   （二）定基指数数列和环比指数数列
   定基指数数列——是指由一系列定基指数按时间先后顺序排而成的。
   环比指数数列——是指由一系列环比指数按时间先后顺序排而成的。
   一般来讲，定基指数数列的编制，更有利于研究现象的动态发展趋势，而环比指数数列的编制，则更适用于分析现象短期的（即前一期的）动态变化情况。下表反映了定基指数数列和环比指数数列的编制方法。
                     
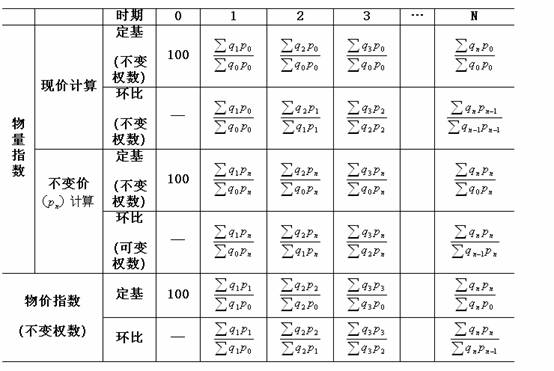
   （三）数量指数数列和质量指数数列
   （四）定基指数和环比指数间的关系
   在指数数列中，由于指数的种类和权数不同，因而两者之间的联系也不相同。在总指数数列中，只有采用不变权数的条件下，环比指数的连乘积才等于相应时期的定基指数。即：
                                 
   这里应指出：不变价格不是始终不变的，当遇到不变价格更新时，必须先计算出换算系数。假定已经知道 2000 年按 1980 年 不变价计算的产量指数，要知道 2000 年按 1990 年计算不变价计算的产量指数，就应当先算出换算系数。该换算系数公式如下：
                                   
   再用这个系数去乘过去年份按 1980 年不变价格计算的产值，即可换算成按 1990 年不变价格计算的产值，这可以消除不变价格变动的影响；否则，编制的产品产量指数缺乏可比性。