当前位置:课程学习>>第三章 行列式>>本章练习
1.决定以下![]() 级排列的逆序数,从而决定它们的奇偶性:
级排列的逆序数,从而决定它们的奇偶性:
1)![]()
2)![]()
2.选择![]() 与
与![]() 使
使
1)![]() 成偶排列;
成偶排列;
2)![]() 成奇排列.
成奇排列.
3.写出把排列![]() 变成排列
变成排列![]() 的那些对换.
的那些对换.
4.决定排列![]() 的逆序数,并讨论它的奇偶性.
的逆序数,并讨论它的奇偶性.
5.在![]() 级行列式中,
级行列式中,![]()
![]()
![]()
![]()
![]()
![]() ;
;![]()
![]()
![]()
![]()
![]() 这两项应带有什么符号?
这两项应带有什么符号?
6.写出![]() 级行列式中所有带有负号并且包含因子
级行列式中所有带有负号并且包含因子![]() 的项.
的项.
7.按定义计算行列式:
1) 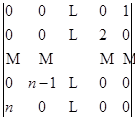 ; 2)
; 2) 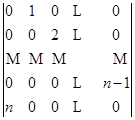 ;
;
8.由行列式定义证明:
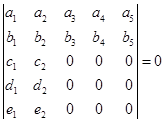 .
.
9.由行列式定义计算
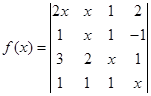 中
中![]() 与
与![]() 的系数,并说明理由.
的系数,并说明理由.
10.由 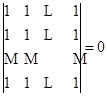 .证明奇偶排列各半.
.证明奇偶排列各半.
11.设
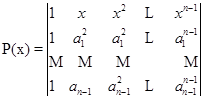 ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() 是互不相同的数.
是互不相同的数.
1) 由行列式定义,说明![]() 是一个
是一个![]() 次多项式;
次多项式;
2)由行列式定义,求![]() 的根.
的根.
12.计算下面的行列式:
1) 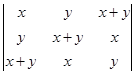 ;
;
2)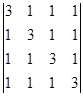 ; 3)
; 3) 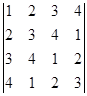 ;
;
13.证明
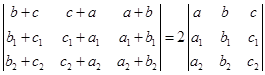 .
.
14.计算出下列行列式的全部代数余子式:
1) 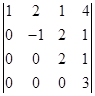 ; 2)
; 2) 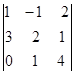 ;
;
15.计算下列![]() 级行列式:
级行列式:
1) 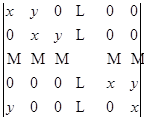 ;
;
2) 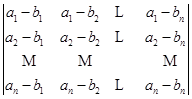 ;
;
3) 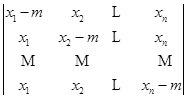
4) 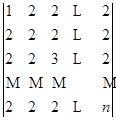
16.证明:
1) 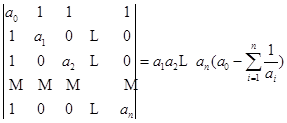 ;
;
2) 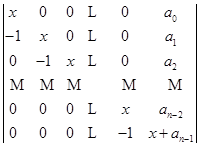
![]()
3) 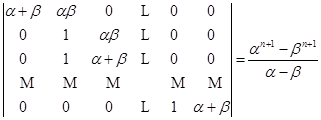
4) 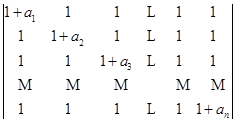
![]()
17.用克拉默法则解下列线性方程组:
1)  2)
2) 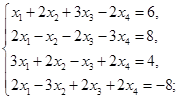
18.设![]() ,
,![]() ,
,![]() ,
,![]() 是数域
是数域![]() 中互不相同的数,
中互不相同的数,![]() ,
,![]() ,
,![]() ,
,![]() 是数域
是数域![]() 中任一组给定的数,用克拉默法则证明:存在唯一的数域
中任一组给定的数,用克拉默法则证明:存在唯一的数域![]() 上的多项式
上的多项式![]() 使
使
![]() ,
,![]() .
.

