2. 测量数据的检验
对测量数据，往往需要检查它的可靠性，以确定测量仪器等是否可靠，方法有两种，如下述。
（1）直接检验
对一组测量数据可以把它们直接计算的和按理论分布求得的误差进行比较，从而检验这组数据是否符合理论分布，现举一例说明。
用G—M计数器测量一组本底计数，每次测1份，所得数据如下：
29
37 27 33 35 32
36 35 24 30 30 23
19
29 32 27 27 27
26
30 21 28 25 33
24
34 14 30 24 24
其平均值
计数/分
按标准误差的一般计算公式计算标准误差得
为
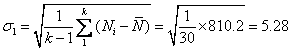
根据核衰变统计误差求得
为：
比较和可见用两种算法得的标准误差相近，这说明测量中除统计误差外不存在其他因素造成的误差。这是因为反映的是所有因素（除统计涨落外还包含其他偶然误差）造成的数据离散程度，只反映了统计涨落造成的离散，两者一致说明了除统计涨落外不存在其它误差，仪器及测量可靠。
（2）频率直方图法
测量一组数据（往往量较大），把一组测量数据，按一定区间分组，统计测量结果出现在各区间的次数
或频率/总次数（k），以次数或频率/k作为纵坐标，以测量值为横坐标这样作出的图形在统计学上称为频率直方图时。见图3-7。频率直方图可以形象地表明数据分布状况。为了便于与理论分布曲线比较，建议在作频率直方图时，将平均值置于组中央来分组，组距为
/2，各组的分界点是
、
、
……
各组的中间值为
、
、
……
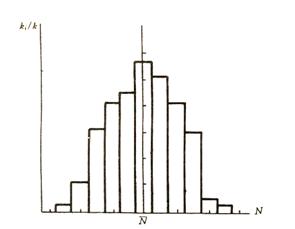
图3-7
3.测量时间的选择
在实际测量中常遇到两次测量数的相加、减或乘、除等，若两数为
，则它们
相加时为
相减时为
相乘时为
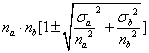
相除时为
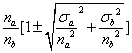
进行放射性测量，在每次测量的数据里，实际上包含本底计数，设
为源加本底的计数率，
为本底的计数率，
为源的计数率，则有
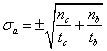
相对误差为
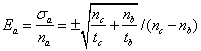（3.6）
可见，本底越大，对测量的准确度的影响也越大，测量的时间越长，精度越高。因此，在测量中要保持较小的本底和较长的测量时间。但是，我们不能无限制地延长测量时间，而应该根据准确度的要求选择合适的测量时间，使得相对误差有最小值，即必须满足条件
因
（
为常数），把（3.6）式代入上式得
由此得出 
或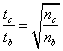 
（3.7）
即合理的分配测量源加本底的时间和测量本底的时间，便满足
将（
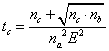（3.8）
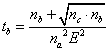（3.9）
式中
。如果已知本底的计数率和源加本底的计数率，则可由（3.8）和（3.9）式求出所需要的测量时间
及
，使测量能满足所要求的相对误差
。
当本底和放射源的计数率之比小于给定的准确度（即
）的情况下，（3.8）和（3.9）可近似地写为
（3.10）
（3.11）
即本底可忽略不计。
[实验装置]
实验装置的方框图如图3-1所示。它包含FJ-365型
探头，探头盒，脉冲示波器及FH