克鲁捷茨基根据大量的实验,得出结论:概括能力强的学生具有最大限度概括的特点,特别表现在概括的广度和速度上。他们能够迅速发现隐藏在具体细节后面的普遍性,看到隐蔽在外部表面现象深处的本质关系,排除干扰,找出那些主要的、基本的关系和结构,并从中发现熟悉的模式。而熟悉的模式与已有经验相呼应,为解题提供了思路。
③通过直觉、逻辑的思考,寻找和探索解决问题的途径的能力。当面临一个问题情境时,我们要想很快地探索出一条解题途径,必须具有心理过程的灵活性、机动性等思维品质,以及掌握合情推理与逻辑论证有机结合的思维方法。
心理过程的灵活性、机动性表现为自由而轻易地从一种心理运算转向另一种性质不同的心理运算。在具体的解题过程中表现为,探索起点灵活,能从多方面去试探问题的解法;探索过程灵活,摆脱定型化的、惯用的解题方法的束缚影响,不费力地重新组合建立了的思想模式和运算系统。正确掌握合情推理和逻辑论证的有机结合的思维方法,也对解题途径的探索起着一定的作用。
例2—7:有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需30元;若购甲4件,乙10件,丙1件,共需40元。现在购甲、乙、丙各一件共需多少元。
解:设购甲、乙、丙一件各需X元、Y元、Z元,得
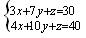
将上述方程组转化为:
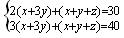
解得: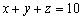 (元) (元)
在教学中,教师要鼓励学生用非常规的方法解题,思维灵活性的反面是思维的呆板性。知识和经验经常被人们按着一定的、个人习惯的“现成途径”反复认识,这就产生了一种先入之见,使思维倾向于某种具体的方法和方式,使人在解题的过程中总想遵循业已知道的规则系统——这既是思维的呆板性。
例2—8:已知二次方程(a-b)x2+(c-a)x+(b-c)=0(a,b,c∈R)有相等实根,求证a,b,c成等差数列。”
对此题,若学生思维呆板,则会总是停留在利用一元二次方程根的判别式上,而不能根据本题条件,得出其它证法;而思维灵活的学生,则能从观察该方程的特点入手,立刻得知该方程的相等实根为1,于是由韦达定理得(b-c)/(a-b)=1从而立即得出2b=a+c ,所以a,b,c成等差数列。得证。 |