定义4.2 （模糊集的运算）
下面继续学习模糊集运算
设A和B分别是U上的两个模糊集，其隶属函数分别为µA和µB，则对于所有µ∈U，存在下列运算：
①A与B的并（逻辑或）记为A∪B，其隶属函数定义为
µA∪B（µ）=µA（µ）∨µB（µ）=max{µA（µ），µB（µ）} （4.10）
②A与B的交（逻辑与）记为A∩B，其隶属函数定义为
µA∩B（µ）=µA（µ）∧µB（µ）=min{µA（µ），µB（µ）} （4.11）
③A的补（逻辑非）记为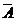
，其隶属函数定义为
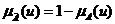（4.12）
例4.4 设U={1，2，3}，F和G分别是U上的两个模糊集，即
F=小=1/1+0.6/2+0.1/3
G=大=0.1/1+0.6/2+1/3
则F∪G=（1∨0.1）/1+（0.6∨0.6）/2+（0.1∨1）/3=1/1+0.6/2+1/3
F∩G=（1∧0.1）/1+（0.6∧0.6）/2+（0.1∧1）/3=0.1/1+0.6/2+0.1/3
=（1-1）/1+（1-0.6）/2+（1-0.1）/3=0.4/2+0.9/3
从这个例子可以看出，两个模糊集之间的运算实际上就是逐点对隶属函数作相应的运算。
设U与V是两个普通集合，U与V的笛卡尔乘积为
U×V ={（u，v）∣u∈U，v∈V} （4.13）
所谓从U到V的关系R，是指U×V上的一个子集，即
R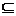
U×V
记为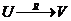
对于U×V中的元素（u，v），若（u，v）∈R，则称u与v有关系R；若（u，v）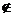
R，则称u与v没有关系。
例4.5 设V={1班，2班，3班}，W={男队，女队}
则V×W中有6个元素，即
V×W={（1班，男队），（2班，男队），（3班，男队），（1班，女队），（2班，女队），（3班，女队）}
其中，每个元素是一代表队。假设要进行一种双方对垒的循环赛，则每一个赛局都是V×W中的一个子集，它构成了V×W上的一个关系。
