|
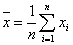
③数学期望:指当测量次数n趋向无穷大(n→∞)时算术平均值的极限。用x∞表示:
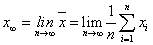
(2)系统误差和随机误差的表示
系统误差是指测定值的数学期望与真值之差用ε表示。
ε=x∞-x真值
随机误差是指n次测量中各次测量值x与测量数学期望之差。用σi表示:
σi = xi -x∞
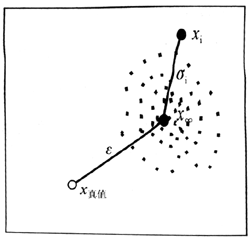
图-8
图-8是x真值、x∞和xi关系的示意图。从图中得知,随机误差σi说明各次测量值与x∞的离散程度,即精密度,σi越小说明数据的重复性好、精密度高;而系统误差ε可做为x∞与真值x真值偏离的尺度,ε越小,即准确度越高。
(3)平均误差与标准误差的表示
①平均误差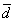 可用下式表示: 可用下式表示: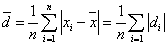
其中: ;用平均误差表示测量误差,计算方便,但由于采用平均值的方法,容易掩盖个别质量不高的测量。 ;用平均误差表示测量误差,计算方便,但由于采用平均值的方法,容易掩盖个别质量不高的测量。
②标准误差σ又称均方根误差。
 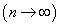
通常真值x真值是未知的,而且测量次数n有限,这时可以用贝塞尔(Bessel)式得出在有限次测量情况下,单次测量值的标准离差S,且把测量的标准离差(S)作为标准误差(σ)的估计,σ≈S,这样标准误差σ就表示为:

(4)绝对误差与相对误差的表示
绝对误差是测量值与真值之间的偏差,某次实验的绝对误差可用下式计算:
绝对误差=测量值-真值
视测量值与真值相比较大小不同,绝对误差可以是正值,也可以是负值,它的单位与测量的单位相同。
相对误差是绝对误差与真值的比值(百分数表示),某次实验的相对误差可用下式计算:

相对误差是无因次的,因此不同物理量测量的相对误差可以互相比较,它是一种常用的评定测量结果优劣的方法。相对误差也有正、负值之分。
由于在一般情况下真值是不知道的,故在实际使用时,真值一般用手册中查得的数值或由理论计算所得的值代之。
4.测量结果的表示
(1)坏值及其剔除
多次反复测量中,由于种种原因使个别测量值较为分散,若保留这一数据可能使结果误差较大,能否将其舍去:下面介绍两种判断的方法。
①3σ法则:由统计规律可知,在多次测量中,任意一个测量值x在(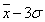 , ,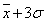 )范围内出现的机会为99.7%,因此在( )范围内出现的机会为99.7%,因此在(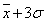 )<x,x<( )<x,x<(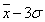 )范围内出现x值是不大可能的,所以定义( )范围内出现x值是不大可能的,所以定义(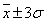 )为测量值的范围大小,3σ为误差界,故误差 )为测量值的范围大小,3σ为误差界,故误差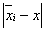 超过3σ的测量即为粗差,可以舍去。该法则的缺点是在测量次数较少(n≤10)的情况下,若用3σ作为粗差识别标准,则可能剔不出粗差。 超过3σ的测量即为粗差,可以舍去。该法则的缺点是在测量次数较少(n≤10)的情况下,若用3σ作为粗差识别标准,则可能剔不出粗差。
②肖维勒准则:肖维勒准则可以满足测量次数较少时的粗差剔除。肖维勒准则认为:对相同精度相互独立测量所得数值,若测量值xi满足: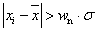 时,即xi即为粗差,应给于剔除,式中wn与测量值的测试次数n有关,其值见表-3。 时,即xi即为粗差,应给于剔除,式中wn与测量值的测试次数n有关,其值见表-3。
表-3 肖维勒系数wn数值表

以上两种坏值剔除方法,均要注意以下二点:
⑴在进行判断时,计算平均值要包括在可疑值。
⑵结果确定了可疑值要弃去,在剔除可疑值后,要重新计算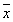 及σ时,只有剔除可疑值后的计算结果才能符合:可靠率99.7+危险率0.3%=1。 及σ时,只有剔除可疑值后的计算结果才能符合:可靠率99.7+危险率0.3%=1。
剔除坏值应是极个别的,否则应从实验方法和技术上查找原因。
┆1 2 3 4┆下一页┆
|