溶剂凝固点测定的结果表示为：（5.797±0.005）
　 溶液凝固点T测量三次，其读数分别为5.500、5.504、5.495，按上述方法计算可求得溶液凝固点测定的结果表示为：5.500±0.003。溶液凝固点降低数值可表示为：
　　　　T^*_f－T_f＝(5.797±0.005)－(5.500±0.003)＝（0.297±0.008）。
　 从中可知：凝固点降低的平均值为△T_f =0.297，
　　　　　 凝固点降低测量的平均误差△(△T_f) =±0.008。
　 当以平均误差表示最终结果时，写为M±△M；其中M为分子量的测定值，△M为分子量测定经传递的平均误差。因为
　　　　　　　
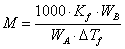
　 依平均误差传递公式：
　　　　　　　　
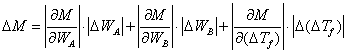
　 式中
　　　　
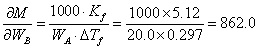
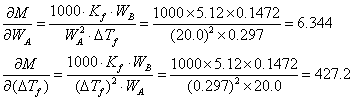
　 代入平均误差的传递公式得
　 △M＝862.0×0.0002＋6.344×0.05＋427.2×0.008 = 3.907≈4
　 　　　　　　
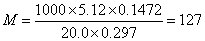
　 最终结果表示为：M=127±4（g/mol）
　 6．实验误差的估计
　 根据被选定的实验内容和实验体系，分析所用仪器及实验步骤中可能产生最大误差的因素，从而引起操作上的注意，这种分析称为对实验误差的估计。这种估计可以为选择仪器装置及试剂等级提供依据。
　 以下以“凝固点降低法测分子量”实验加以说明如何估计实验的误差。
　 在此实验中，用台秤称量溶剂，分析天平称量溶质，并用贝克曼温度计测量凝固点的降低值，从表－3中得到函数关系为乘、除时被传递的相对平均误差的公式，可推知，分子量测定的相对平均误差为：
　　　　　　　　
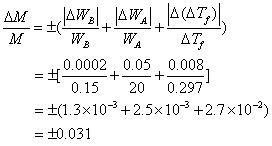
　式中0.0002克为分析天平称量溶质时的绝对误差，0.15为溶质克数；0.05克为台秤称量溶剂时的绝对误差，20为溶剂克数；0.008是用贝克曼温度计测量凝固点降低值时（溶剂、溶液各测量三次）带来的绝对误差，0.297为凝固点降低的值；上式看出，当在实验时，使用上述仪器，实验最大的相对误差为3.1%。
　 若用刻度为1/10的温度计代替刻度为1/100贝克曼温度计，当其他条件不变时，按每次测温的绝对误差都增大10倍计，则
　　　　　　　　　
　　　　　　　　　
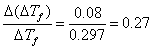
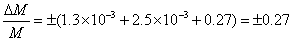
　　即此时测定分子量的相对误差从3.1%升到27%，很明显，所得分子量测定结果误差太大，改用刻度1/10的温度计测量显然是不适宜的。
　 同样，提高溶剂称量的精度，而其他条件不变时改用分析天平来称量溶剂时，称量的精度从0.05g提高到0.0002g，则：
　　　　　　　　　
　　　　　　　　　　
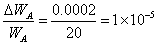
　计算表明，这时对分子量的测定的相对误差从3.1%降到2.8%，对最后结果影响并不太大，很显然，不必要用分析天平称量溶剂。
　 同样，对于溶质的称量，由于溶质少，所以用分析天称量是必要的。但是，溶质计量的精度如果稍有降低，对测定结果影响也并不太大，例如当称量精度降低一倍，即其误差为△WB=0.0004时，则：
　 　　　　　　　　
　　　　　
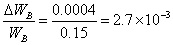
　 可见称量溶质精度降低一倍，最大相对误差只从3.1%增大到3.2%，只增加了0.1%，因此在此实验中，往往可以加入少量固体溶质作为凝固过程的晶种，以避免过冷现象出现而影响温度读数的精确性，这种做法的结果往往反而提高实验的精确度。
　 以上分析说明，在此实验中测温的精确度（包括温度计的精度和操作技术条件）是造成这种误差的主要原因，如果要提高用凝固点降低法测分子量的精确度，首先要考虑提高测温的精确度。反之，测温精确度的降低必将大大增加分子量测定的误差。
　 事先估计各项所测的误差及其影响，将指导选用精密度适宜的仪器和选择正确的实验方法，控制适宜的条件并抓住测量的关键，从而得到精密度较高的实验结果。
　　　　　　　　　　　　　　　　　　　　　　　　　　 　┆1 ２ ３ ４┆