|
(2)测量结果精密度和准确度的表示
精密度是表示各观测值相互接近的程度,即表示每次测量的重复性,用平均误差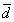 或标准误差σ表示,物化实验中测量结果的精密度表示为: 或标准误差σ表示,物化实验中测量结果的精密度表示为:
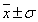 或 或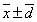
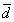 或σ越小,表示测量的精密度越好。 或σ越小,表示测量的精密度越好。
有时也用相对值直接表示相对精密度。
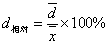 ; ;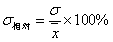
准确度是表示观测值与真值接近的程度。若用x真值代表真实值,xi为第i次测量时所得的测量值,n为测量次数,物化实验中测量结果的准确度b可用下式表示:
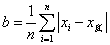
在大多数情况下,x真值得很难得到的,实际上,常用某种更为可靠的方法测得的数值x标(或从手册中查得)来代替x真值,故测量结果的准确度可近似地表示为:
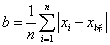
从上述可知,精密度和准确度两个概念既有严格的区别,又有一定的联系。在物化实验中,必须注意使用仪器(如移液管、容量瓶、天平等)的精密度。使用温度计时一般取其最小分度值的1/10或1/5作为其精密度,例如1度刻度的温度计的精密度可估读到±0.2K,1/10刻度的温度计的精密度可估读到±0.02K。
5.误差的传递
大多数的物理化学数据的测量,要对几个物理量进行测量,通过函数关系加以运算,才能得到所需要结果,如在凝固降低法测分子量实验中,溶质分子量M为
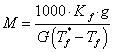
M为间接测量,每个直接测量量(如g、G、 、Tf、)的误差都会影响最终测量结果(M),这种影响称为误差的传递。从测量结果的表示式( 、Tf、)的误差都会影响最终测量结果(M),这种影响称为误差的传递。从测量结果的表示式(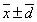 或 或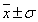 )看,关键是要了解直接测量量的平均误差( )看,关键是要了解直接测量量的平均误差(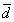 )或标准误差(σ)是如何传递给间接测量量的。这里仅介绍平均误差的传递。 )或标准误差(σ)是如何传递给间接测量量的。这里仅介绍平均误差的传递。
设有函数:N=f(u1,u2,……,un),其中N由u1,u2,……,un各直接测量值所决定。
现已知测定u1,u2,……,un时的平均误差为△u1,△u2,……,△un,求间接测量量N的平均误差△N为多少?
对N全微分得

设各自变量的平均误差△u1,△u2, ……,△un足够小时,可代替它们的微分du1,du2,……,dun,考虑到在不利的情况下是直接测量的正负误差不能对消,从而引起误差的积累,故取其绝对值,则间接测量量N的平均误差△N为:
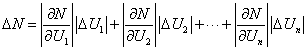
由此可见,应用微分法直接进行函数平均误差的计算是较为简便的。部分函数的平均误差及相对平均误差列于表-4

误差的传递计算举例
以下用凝固点降低法测分子量的例子说明平均误差传递的计算:以苯为溶剂,用凝固点降低法则定萘的分子量,按下式计算:
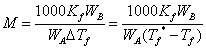
式中凝固点降低常数Kf可查表得出:Kf=5.12,而直接测量值为WB、WA、Tf*、Tf;其中,溶质质量WB为0.1472g,若用一等分析天称重,溶质质量测定的绝对误差为△WB=0.0002g,溶剂质量WA为20g,若用工业天平称重,溶剂质量测定的绝对误差为△WA=0.05g。
测量凝固点降低值,若用贝克曼温度计测量,其精密度为0.002,测出溶剂的凝固点Tf*三次的读数,分别为5.800,5.790,5.802,则:
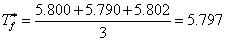
各次测量偏差:
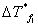 =5.800-5.797=+0.003 =5.800-5.797=+0.003
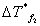 =5.790-5.797=-0.007 =5.790-5.797=-0.007
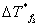 =5.802-5.797=+0.005 =5.802-5.797=+0.005
溶剂凝固点测定的平均误差为:
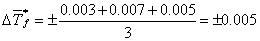
┆1 2 3 4┆下一页┆
|