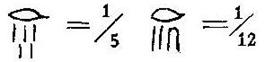|
分数：[1]埃及人对分数的理解和记法都比今日复杂得多。他们把 随着计算方法的不断改进，分数范围的不断扩大，用“单位分数”(分子是1的分数)来表示分数；
对一般分数，则拆成“单位分数”表示[2]。例如：(用现代符号表示)
2. 代 数 在纸草书中含有一次方程的解法。在埃及语中，把发“哈喔”(hau)音的算法，称作“阿哈算法”。[3]此法与现在解含有一个未知量的一次方程式是完全类似的。 埃及人对“级数”有了一定的认识，在纸草书第79题中，写出一列数7，49，343，2401，16807，以及与这列数对应的一列词。“图画”，“母猫”“老鼠”，“大麦”，“容器”。并给出和数是19607。这种表示是公比为7的等比数列。对此有人解释为：“有7个人，每人有7只猫，每只猫能吃7只老鼠，而每只老鼠吃7穗大麦，每穗大麦可以长出7容器大麦。埃及人从这个题目中可以写出怎样的一列数，它们的和是多少。”[4] 3. 几 何 埃及人的几何是以适用工具为特征，以求面积和体积为具体内容。他们提出了计算土地面积，仓库容积、粮食堆的体积、石料和其它建筑材料多寡等法则。 关于面积的计算。埃及人能应用正确的公式来计算三角形、长方形、梯形的面积。把三角形底边二等分，乘以高。同样，把梯形两平行边之和二等分，乘以高分别作为三角形和梯形的面积，并且，能对不同的面积单位进行互相换算。 在埃及埃特夫街的赫尔斯神殿的文书中，有很多关于三角形和四边形面积计算问题[5]。但是，他们把四边形二对边之和的一半与另二对边一半之积作为其面积[6]，这显然是不对的，只是在四边形是长方形时，这才是正确的结果。
圆的面积的计算当时达到了惊人的程度，他们使用公式：
[1] 参照K.Sethe，VonZahlen und Zahlwörtern bei den a|ten Agyptern und was für andere Vö1uer und Sprachen daraus zu lernen ist, Schriften der wissenschaftlichen Geselschaft Strassburg 1916.
[2]
要注意，将分数表示成单位分数是不唯一的。如 [3] [日]村田全、佐藤胜造译B. L Vander Waerden《数学的黎明》一书中，称“ァハ算法” [4] 参照[苏]B. B. 鲍尔加尔斯基著潘，德松、金钊译《数学简史》P26 [5] Lepsius Abh preuss Akad Wiss Berlin 1855；Philos-hist Abteilung p69
[6]用现代符号a与b以及c与d分别表示两批相对的边，其面积为
|
理解为“二个部分”(the two
parts)，并且，把能使“二个部分”变成整体的部分叫做“第三部分”(the third part)
，(其中
是圆的直径)。由此，得到
