关于体积的计算。埃及人已知道算立方体、箱体、柱体和一些简单图形体积的方法。他们知道了立方体、直棱柱、圆柱的体积为“底面积乘以高”。

埃及几何中，最突出的一项工作是发现截棱锥体的体积公式。当锥体的底是正方形时，这个公式用现代的记号表示为：

  (1)

其中是高，和是上、下底的边长。

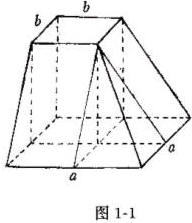
像这样的公式，被认为是靠经验得到的，是不可理解的。这似乎是通过理论推理完成的。对此可作如下探讨：

把正棱台分成四个部分，即一个长方体二个棱柱，一个棱锥，如图1—1，假如棱锥的体积是已知的，可得公式：

                  (2)

可推测(1)式是由(2)式的代数变形得到的。但是，埃及人善长于具体数值的计算，还不能进行一般量的推导。在此，可考虑埃及人是否受巴比伦代数的影响[1]。

从公式(2)推出公式(1)的方法，也可作如下推测：

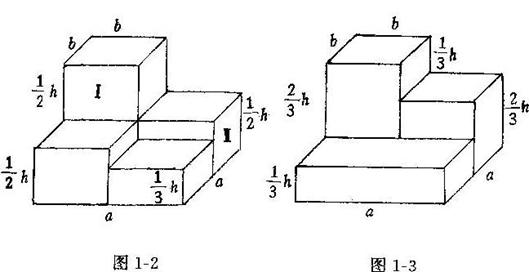
假定一个棱垂直于底面，把图1—2中的两个棱柱分别变为高是原来一半的长方体、再把棱锥变为高是原来的长方体，如图1—2。然后，在其三个长方体中，把第1个从上部截取放到第Ⅱ个上面，如图1—3。这样，得到的立方体的高分别为，由三个水平层，其最下层的底面积为’，中间层的底面积是，最上层的底面积为，可得到其总体积为：与(1)式相符。