 |
         |
当前位置：首页→进入课程-课程学习→教学内容-第四章 数学学习的特殊过程
章节导航 |
|||||
|
绪 论 第一章 第二章
第一节 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章 |
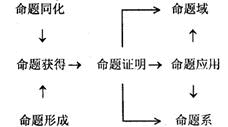
( 二 )数学命题的学习过程 在一个演绎系统中，不需要证明而把它们作为判断其他命题的真假的初始命题称为公理。从公理或从已被证明的其他真命题出发，用逻辑推理的方法推导出来，并可进一步作为判断其他命题真假的依据的真命题，称为定理。数学中的公式也可作为命题的一种形式。公式一般是指用数学符号表示几个量之间的关系的式子，它具有普遍性，适用于同类关系的所有问题。数学中大量有明确结论的习题也可作为数学命题。一部分带有探索性或创造性的问题，以及一些可以构成多种真命题的开放性命题都是数学命题的组成部分。 我们将数学公理、定理、法则、公式等内容的学习，称为命题学习。其目的是为了掌握这些数学命题，并能应用数学命题解决实际问题，或为进一步学习其他数学命题做必要的准备。命题是由概念或一些更简单的命题复合而成的，因而命题学习的复杂程度高于概念学习。 1. 数学命题学习的主要形式 数学命题学习主要有以下两种形式： （ 1 ）数学命题发现学习 发现学习是学生独立地获得知识的学习方式。学生从具体例子出发，通过操作、实验、分析、推理，发现一般结论。 数学命题发现学习的过程大致有以下几个环节：①探索发现；②提出假设；③验证假设；④得出结论；⑤理解和应用。 （ 2 ）数学命题接受学习 接受学习是将学习的内容以定论的形式呈现给学生，学生将这些内容加以内化。 数学命题接受学习的过程大致有以下几个环节：①分析命题；②激活旧知识；③证明命题；④理解和应用。 数学命题发现学习和接受学习两种形式各有利弊，发现学习有助于培养学生的探索精神，但要花费较多的时间。接受学习是由教师控制的，它比较紧凑，节约时间。但在对激发学生学习的兴趣引起学生对实际问题的关注等方面又显得不足。教师应根据所学命题的特点选择适当的学习形式。 奥苏伯尔将有意义学习分为五类：表征学习、概念学习、命题学习、解决问题的学习与创造学习。奥苏伯尔将命题学习单独列为一类学习，而且又根据原有观念 ( 命题 ) 与新观念的关系，将命题学习的形式分为三类，即下位学习、上位学习和并列学习，这样就对命题学习进行了比较细致的刻画。 2 . 数学命题学习的阶段 数学命题学习分为命题获得、命题证明和命题应用三个阶段，最终使个体形成命题域和命题系。 （ 1 ）命题获得 命题获得通常采用两种方式 : 一种方式是同化形式，即直接给学习者展示要学习的新命题，学习者原有观念与新命题中的各有关概念联系起来，这种联系的最初阶段是刺激与反应的联结，学习者要在工作记忆中将一些激活的结点联结起来，然后将新命题纳入认知结构，对原来的认知结构进行改组和加工，形成新的认知结构。显然，这是一个对信息的加工过程。命题获得的另一种形式是命题的形成，即学习者通过考察命题的特例，然后抽象、概括命题的过程。例如，要学习命题 :a+b=b+a 。该命题的教学不是先给出命题，而是先让学生考察一些特例， 1+2=3,2+1=3,1+2=2+1;4+5=9,5+4=9,4+5=5+4; …，让学生通过对特例的证明进而观察出这些特例的共同特征 : 加数与被加数可以交换，而和不变。这样便可抽象概括出一般性命题。可见，命题形成是一种上位学习的形式。 命题同化所对应的学习方式是接受式，其学习过程包含刺激一一反应的联结和对信息进行加工的认知因素，如果学习者只是完成了联结的心理过程而没有同化过程，那么这种学习就是机械学习，而只有将新命题纳入认知结构，才能成为意义学习。一般说来，命题同化的学习方式在命题获得阶段为学生提供的主要是知识的信息。命题形成对应的学习方式是发现式，学习心理是以辨认、分化、假设、验证、抽象、概括等为主的一系列认知加工过程，给学习者提供的不仅包括知识信息，而且还包括智能信息。 命题获得是命题学习的第一阶段，要使命题表象进入长时记忆从而形成命题域和命题系，必须经过命题的证明和应用两个阶段去强化。 （ 2 ）命题证明 命题的证明是下位学习形式，即要利用已学过的某些命题来推当前命题，其心理过程可以用激活扩散模型给予解释。首先，学习者通过命题同化或形成方式获取命题，并将该命题作为结点纳入认知结构适当的命题域 ( 系 ) 中，然后激活相联的有关命题或概念，并对每一个激活的结点进行评判，选择合适的结点连成一条欲证命题的题设和结论之间的通路，一旦通路形成，命题即得证明。由于命题域 ( 系 ) 中命题间的连线按联系的紧密程度而有长短之分，激活的强度又会受到个体选择结点的加工策略制约，这样就会造成连线长、强度弱的结点难以利用，从而造成命题证明难易程度不同的情形。 在具体的教学中，命题证明这一过程的学习主要在教师引导下完成的，提供给学习者的主要是智能信息。在理解命题的过程中，学习者要以已获得的原有若干命题为逻辑依据，同时将新命题纳入认知结构，于是形成一个关于新命题的不太稳定和不十分清晰的命题域和命题系，其保持依赖于命题的应用。 （ 3 ）命题应用 命题的应用包括两方面，一是数学命题在解决数学问题中的应用，二是数学命题在解决实际问题中的应用，这里我们只讨论前者。 我们将公式、法则称为程序性命题，把不含公式、法则的公理、定理称为推理性命题。这样，命题的应用就相应地分为程序性命题的应用和推理性命题的应用。 程序性命题，实质是解决一类问题的规则和程序，个体在程序性命题的应用中，只需将待解决的问题输入工作记忆再与长时记忆中的命题联系起来，进行一种较简单的模式识别，然后按照规则和程序操作即可解决问题。而在推理性命题的应用中，个体则需要进行模式识别、策略选择、激活扩散等一系列的信息加工，而且还要受到元认知的调控，解决问题往往伴随着“顿悟”的过程，如果说程序性命题应用的一个功能在于训练学生的智慧技能，那么推理性命题应用的一个功能则在于发展学生的数学能力。 要对命题有更深层次的理解，在命题应用中形成命题域和命题系是至关重要的。 例如，对于命题 : 3. 命题学习的本质 综上所述，数学命题学习过程可表述如下 :
数学命题学习的整个心理过程包含着刺激一反应的联结因素和信息加工的认知因素。数学命题学习是一个知识信息获取和智能信息获取并存的过程。数学命题学习的高级目标是通过上、下位学习，同位学习，并列学习从而形成个体的命题域和命题系，改组、丰富和完善个体的认知结构，这就是数学命题学习的本质。 |
||||
。要对该命题有深刻理解，就应把握与此相关的一些等价命题 . 如
。
等等。进一步，还应掌握该命题的一些弱抽象命题。如 :
, n 为偶数，
, 则当且仅当 a=0 且 b=0 等等。这样就形成了个体的命题域和命题系，逐步完善了认知结构。由此可见，数学命题的应用是在使学生获得智能信息的同时，逐步形成稳固的命题域和命题系，充实和完善个体认知结构的过程。
视频课堂第四章 |
第一节 数学知识的学习 |
|