|
章节导航 |
||||||||
|
绪 论 第一章 第二章
第一节 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章 |
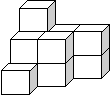
第三节 空间观念及其培养 《标准》在总目标中明确提出“通过义务教育阶段的数学学习,学生要能够具有初步的创新精神和实践能力, … ”。根据数学的学科和课程特点,《标准》把“空间观念”作为义务教育阶段培养学生初步的创新精神和实践能力的一个重要学习内容。《标准》对空间观念所作的阐释,以及在相关内容上所做的具体安排,充分体现了《标准》总目标对培养创新精神的要求。 传统的几何课程,内容差不多都是计算和演绎证明,到了初中以后,几乎成了一门纯粹的关于证明的学问。之所以如此,与我们传统上认为“数学是思维的体操”、把智力或思维能力的发展看成数学教育的主要目标有关。但是,以证明为主题的几何课程内容主要是由一些经过精心组织、现成的、条理清晰的概念、公理、定理和逻辑的思考方法(主要是三段论)构成的,重点在形式化,内容比较单调,呈现方式也是冷冰冰的。这样的课程难以鼓舞学生的学习欲望和兴趣,学习这样的课程时,学生只能是被动的参与,难觅发挥主动性和创造性的空间。另外,传统的几何课程中很难找到与“空间”有关的内容。虽然“教学大纲”也有关于“空间观念”的表述,如“能够由形状简单的实物想象出几何图形,由几何图形想象出实物的形状”等等,但在具体的教学内容和教学要求中却鲜见与之有关的解释和说明。几何课程的主旋律就是研究平面几何图形及其性质的基本方法,虽然也有“识图初步”这样的条目,但无论在内容和要求上都显得无足轻重。 然而,空间与人类的生存和居住紧密相关,了解、探索和把握空间能使孩子更好的生存、活动和成长。空间观念是创新精神所需的基本要素,没有空间观念,几乎谈不上任何发明创造。因为,许许多多的发明创造都是以实物的形态呈现的,作为设计者要先从自己的想象出发画出设计图,然后根据设计图做出实物模型,再根据模型修改设计,直至最终完善成型。这是一个充满丰富想象力和创造性的探求过程,这个过程也是人的思维不断在二维和三维空间之间转换、利用直观进行思考的过程,空间观念在这个过程中起着至关重要的作用。所以,明确空间观念的意义,认识空间观念的特点,发展学生的空间观念,对使学生具有初步的创新精神和实践能力是十分重要的。这就是《标准》把“空间观念”作为义务教育阶段重要学习内容的意义。 《标准》描述了空间观念的主要表现,其中包括 “能够由实物的形状想象出几何图形,由几何图形想象出实物的形状,进行几何体与其三视图、展开图之间的转化”。 这是空间观念最基本的表现。这是一个包括观察、想象、比较、综合、抽象分析,不断由低到高向前发展的、对客观事物的认识过程。是建立在对周围的环境直接感知基础上的、对空间与平面相互关系的理解和把握。在这个意义上,空间观念是学生主动的、自觉的或自动化的“模糊”二维和三维空间之间的界限的一种本领,是学生对生活中的空间与数学课本上的空间之间的密切关系的领悟。 把握实物与相应的平面图形、几何体与其展开图和三视图之间的相互转换关系,不仅是一个思考过程,也是一个实际操作过程,把上述表现进一步向前延伸,就是要尝试着物化那些感知到的、在直观的水平上有所把握的“转化”关系,这就是《标准》提到的 “能根据条件作出立体模型或画出图形”,重现感知过的平面图形或空间物体。无论是做立体模型还是画出图形,都要在头脑加工和组合的基础上,通过实际尝试和动手操作来实现。这种重现能使几何事实基于直观的表象、联想和特征得到实实在在的表示,使空间观念从感知不断发展上升为一种可以把握的能力。 进一步,《标准》指出了空间观念在分析和抽象层次上的表现,如“能从叫复杂的图形中分解出基本的图形, …. ”, “能描述实物或几何图形的运动和变化;能采用适当的方式描述物体间的相互关系”等等, 这些表现在把握“相互转换”关系的基础上,刻画了根据图形的特征在逻辑上对图形关系进行的分析与操作。例如,在电话里向别人描述你搭的如下图所示的积木块建筑的形状,就要抓住积木块之间的位置关系,使对方在看不到实物的情况下,通过你的叙述产生符合原形的直观想象。叙述和倾听都需要在逻辑上对图形关系进行的分析与操作。严格准确的描述它的形状,可能会依人的能力差异而有所不同,但这些描述中的共性,可能就导致了一些确定的有规律的内容出现,那就是空间观念。 空间观念的表现还包括“能运用图形形象的描述问题,利用直观进行思考”。直观思考是没有严格演绎逻辑的“形象化”的推理,是结合情景进行的思考。如,根据下面三视图建造的建筑物是什么样子的?共有几层?一共需要多少个小立方体?
回答这个问题,必须多次进行形式如“如果 …… 那么”的思考,尝试得出正确的结论。比较、综合、归纳、模拟、与位置有关的推理、有条理的具体操作等一系列手段在这里都用得上。回答这个问题会运用到典型的数学思维方法,经历典型的数学解决问题过程:提出假设,得出一个结论,证实或否定这个结论,这里虽然没有严密的命题逻辑和演绎推理,与直观结合的思考,照样能得出正确的结论。 培养空间观念要充分考虑以下几个因素。 (一)反映空间观念的课程内容 空间观念不仅是“观念”,还是数学课程里新的内容、题材和呈现方式。由于以往课程中这方面的资源非常缺乏,依据《标准》的要求,选择与空间观念密切相关的题材就显得十分重要,为了培养和发展学生的空间观念《标准》不仅在“空间观念”的提法上加入了一些新的元素,而且在内容上做了相应的安排,在三个学段都大大加强了与培养空间观念有关的内容,提出了一些新的具体目标。如: 第一学段的“辨认从正面,侧面,上面观察到的简单物体的形状”,“会用上下左右前后描述物体的相对位置”,“能辨认从不同方位看到的物体的形状和相对位置”。 第二学段的“认识长方体、正方体、圆柱体的展开图”。 第三学段的“知道物体的阴影是怎么形成的,并能根据光线的方向辨认实物的阴影。”“了解闪点视点 视线及盲区的含义 … ”等等。 这些内容的设置,使视图与构造、直观与推理、观察与投影等这些内容成为了培养学生空间观念的重要学习资源。并且空间和空间观念从孩子入学的那一刻开始就伴随他们成长了。 《标准》中与空间观念有关的内容目标还有很多,这里提到的只是其中的几条,有些是《标准》第一次作为课程内容提出的新元素。在以往的数学课程体系中,这样的内容往往显得无足轻重,有些则完全被屏蔽在数学课程的视野之外。因为按照传统的数学课程理念衡量,这样的内容不那么系统,很难用定义、定理、命题、性质把他们穿起来;这样的内容也不那么好教,一方面严格的逻辑在这里用处不大,另一方面“灌输”的方法也很难起作用;这样的内容更不那么好考,因为探究这样的内容需要观察、思考、交流、模拟、尝试、甚至要争论、辩论、要走出课堂,其中任何一个环节都不大容易在纸上呈现,不大好打分。然而,如果数学课程里没有这些元素,学生的空间观念将从何而来?如果没有空间观念,数学课程将如何满足素质教育的要求、将怎样建立与创新精神培养之间的全面联系?因此,《标准》明确的把空间观念作为与培养学生创新意识有关的重要数学学习内容之一。 |
|||||||