|
章节导航 |
|||||
|
绪 论 第一章 第二章
第一节 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章 |
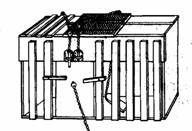
桑代克( Edward Thorndike , 1874-1949 )是美国著名的心理学家,他通过对动物和人的实验研究,首次提出学习过程在于形成一定联结的理论。 他设计了有名的迷箱实验: 把一只饥饿的猫放入设有打开门闩装置的迷箱,迷箱外有一盘食物。在猫第一次偶然打开门闩逃出迷箱之后,又将它放回迷箱,进行下一轮尝试。“逃出—放回”如此重复多次。 桑代克记下猫每次逃出迷箱所需要的时间,发现经过多次连续尝试,猫逃出迷箱所需的时间越来越少,以至到了最后,猫一进迷箱,就能打开门闩,跑出迷箱,获得食物。
桑代克的迷箱装置 桑代克由此否定了顿悟类型的学习,指出如果猫是突然获得观念的话 , 那么学习曲线应呈一种突然改善之势,但是实际上呈现的是一种由慢到快的渐进过程。猫学到的不是观念之间的联结,而是刺激和反应之间的直接联结。行为改进是通过一种机械过程自动地完成的,不需要观念和顿悟。学习是在一种几乎没有意识和思维参与的情况下自动地形成刺激 - 反应联结的过程。 在此实验的基础之上,桑代克提出了他的试误学习理论。 学习即形成刺激 - 反应联结。所谓联结,指的是特定的刺激一定能引起特定的反应( S-R )。 学习是一种渐进的、盲目的、尝试 - 错误的过程,教学则是安排各种情境,以便导致理想的联结并感到满意。人是伟大的学习者,主要因为人可以形成很多的联结,一个人的理智、性格和技能,是他对各种刺激情境及其各种要素作出反应倾向的总和。 桑代克根据动物实验,提出三条学习的定律:准备律、练习律、效果律。 准备律:学习者是否会对某种刺激作出反应,同他是否已做好准备有关。 效果律:只有当反应对环境产生某种效果时,学习才会发生。如果反应的结果是令人愉快的,那么学习就会发生;如果反应的结果是令人烦恼的,那么这种行为反应就会削弱而不是加强。 练习律:包括使用律( law of use )一个已形成的可变联结,若加以应用,这种联结的力量变会增强;失用律( law of disuse )。一个已形成的可变联结,若不予以使用,这种联结的力量变会减弱。 但是桑代克也指出只有当学习者发现重复练习能获得满意的效果时,练习才会有助于学习,没有强化的练习是没有意义的。这样练习律就被消融于效果律中去了。 除了上述三个主要学习律(其中最主要的是效果律)之外,桑代克还提出了一些从属的附律,或称为学习的原则。 多重反应律:学习者对同一刺激情境可能会作出多种多样的反应。当某一反应不能产生满意的效果时,就会作出其他反应,直到有一种反应最终导致满意的效果为止。学习者的学习之所以成功,原因便在于此。在桑代克看来,多重反应的原则至少遍布动物和人类的 90% 的学习中。 定势律:或称“态度”或“顺应”的原则,桑代克在实验中发现,动物可能会以某种特定的态度对待某种外部情境,这取决于它的年龄、饥饿状态、精力状态或瞌睡程度等。反应是学习者态度的产物。 选择性反应律:桑代克发现,有机体在学习时往往会有选择地对刺激情境中的某些要素作出反应,而对其他要素不予理会。鉴于在学习过程中,刺激情境的部分要素便能有效地引起反应,桑代克有时又把这一学习律称为“部分活动”的原则。 同化律:或称“类推”的原则,当有机体对新的刺激情境作出反应时,这种反应往往是与他(它)在以往类似情境中习得的反应像类似的。 联想性转换律:有机体已习得的对一组刺激的反应,可以逐渐转换成对一组新的刺激的反应。具体的做法是:先在刺激情境中加上一些新的刺激成分,然后减去原来的刺激成分,直到只需新的刺激,完全没有原来刺激时也能唤起这种反应为止。 上述几条学习附律都是从动物学习中归纳出来的,但是桑代克还是把它们作为人类学习的基础。另外桑代克还提出了所属律,这是从以人做被试的语言学习实验中概括出来的。此原理是指,如果学习者认识到两个项目在某一方面彼此具有相属关系,那么在它们之间就比较容易形成联结。 桑代克的试误学习理论对数学学习的启示集中表现为三个方面: (一)学生的学习在一定程度上表现为“尝试 - 错误”的过程,只不过学生的“尝试 - 错误”是有目的、有意识的。 (二)根据桑代克的练习律,数学学习中的练习环节不可缺少。 (三)在学习前,要让学生做好充分的准备(包括心理的和生理的,主观的和客观的)。 |
||||