|
章节导航 |
|||||||||||
|
绪 论 第一章 第二章
第一节 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章 |
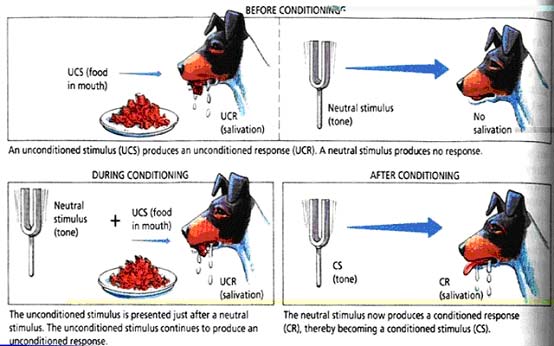
学习心理学是教育心理学的传统领域和核心部分。这一方面与教育实际中的学生是学习的主体有关,另一方面还由于许多心理学家都把学习心理作为教育教学的理论基础看待。因此,在 20 世纪初教育心理学诞生之前,心理学家们就十分重视学习心理的研究。经过近百年的不断发展和完善,学习心理研究已取得了长足的进步,由此引发了一系列教育教学改革。 20 世纪,学习理论经历了从行为主义到认知主义的发展历程: 20 世纪上半叶,行为主义占有主导地位,其基本立场在于:学习研究不应涉及到 不可能观察到的心理过程,而应只局限于可见的行为,这样的研究才是科学的。 美国心理学家桑代克是行为主义的代表人物,他提出了以“刺激—反应联结”和“试误”为主要特点的学习理论,认为学习就是形成刺激—反应联结,这种联结是直接的、无中介的,是在反复的尝试(不断摒弃错误反应,保留正确反应)中所形成的。 桑代克在实验的基础上提出了三条学习定律;准备律、练习律和效果律。在于 1922 年出版的著作《算术的心理学》中他指出,算术无非是一组针对某种数量和关系的特殊化的行为习惯。桑代克的观点为数学学习中的机械练习和训练提供了一定依据。 另一位行为主义代表人物斯金纳 ,他进一步发展了行为主义的主张,提出了操作性条件原理,认为单纯的练习不能保证行为的重复出现,应借助于操作性条件的作用,而这种作用的形成取决于强化,由此,他提出了“刺激—反应—强化”的学习模式,并设计了教学机器和程序教学。斯金纳的理论,为以后教育技术学的发展奠定了一定基础。 从 20 世纪六、七十年代开始,数学学习理论中的认知主义取代行为主义已成必然之势。布鲁纳提出了发现学习理论,强调学习进程是一种积极的认知过程,提倡知识的发现学习。他进行了大量的数学学习实验,并从中总结出四条数学学习原理,即建构原理、符号原理、比较和变式原理、关联原理等。此外奥苏贝尔提出了“有意义学习”理论,加涅提出了“信息加工”学习理论。正是如此众多认知学习理论的出现,使数学心理研究范式发生了重要转变,并预示着认知理论将会有新的发展。 分析研究重要的心理学理论,有助于我们更好地分析研究数学学习心理的特殊规律。 诺贝尔奖金获得者、俄国生理学家伊凡 · 巴普洛夫( Ivan Pavlov , 1870 - 1932 )是最早提出经典性条件反射的人。 他首先用实验方法研究他所命名的条件反射。他关于条件反射的概念、理论对美国行为主义学习理论的建立奠定了基础,行为 主义者华生,格思里等深受他的影响。 巴普洛夫是经典条件反射学说的创立者。巴普洛夫在研究狗的消化生理现象时,把食物呈现在狗面前,并测量起唾液分泌,通常狗吃食物时才会分泌唾液。然而,巴普洛夫偶然发现狗尚未吃到食物,只是听到送食物的饲养员的脚步声,便开始分泌唾液。巴普洛夫没有放过这一现象。他开始做一个实验。先给狗听一个铃声,狗没有反应,然而在给狗铃声之后紧接着呈现食物,并经反复多次结合后,单独听铃声而没有食物,狗也“学会”了分泌唾液。铃声与无条件刺激(食物)的多次结合从一个中性刺激变成了一个条件性刺激,引起了分泌唾液的条件性反应,巴普洛夫将这一现象称做条件反射,即经典条件反射。 一、经典条件反射的形成 条件反射(经典性条件反射):就是某种刺激 - 反应的连续关系的形成。这种刺激 - 反应连续关系的形成,或者会导致有机体的行为模式的持续变化,或者会导致有机体反应的可能性的持续变化。 巴普洛夫认为,反射分为无条件反射与条件反射两种情况: 1 .无条件反射:食物吃到嘴里,引起唾液分泌增加,这是自然的生理反应,不需要学习,这种反应叫做无条件反射;此时引发反应的刺激是食物,为无条件刺激,做出的反应是无条件反应。 2 .条件反射:研究助手的脚步声与狗的唾液分泌增加本来没有必然的联系,是一种无关刺激,或称中性刺激;当脚步声与食物同时、多次重复后,狗听到脚步声,唾液分泌就开始增加,这时中性刺激由于与无条件刺激联结而变成了条件刺激,由此引起的唾液分泌就是条件反应。 狗形成条件反射的机制如下表: 经典条件反射形成的三个阶段
(一)习得 条件刺激与无条件刺激的一次成对呈现称为一次试验,有机体学习这两个刺激之间的联结关系的过程叫做条件反射的习得阶段。 在这一阶段中,条件刺激与无条件刺激呈现的时间可以有三种关系:同时性条件反射、延迟性条件反射与痕迹性条件反射。 在同时性条件反射中,条件刺激与无条件刺激在时间上是完全同步出现的;在延迟性条件反射中,条件刺激先出现一段时间,在它还未消失时,无条件刺激开始出现,然后两种刺激同时消失;痕迹性条件反射中,条件刺激先出现,消失一段时间后无条件刺激才开始出现。 在这三种不同的时间关系中,延迟性条件(条件刺激先出现 0.5 秒)最易形成条件反射;其次是同时性条件反射;再次是延迟时间增长的延迟条件和痕迹性条件反射。如果条件刺激在无条件刺激之后出现,即使有条件反射形成,其效果也是微弱的。 (二)消退 条件反射形成以后,如果得不到强化,条件反射会逐渐削弱,直至消失。例如,狗对铃声形成唾液分泌的条件反射以后,得到了食物(强化),条件反射将进一步巩固;如果只给铃声不给食物,已经形成的条件反射就会消退。这种无强化的条件刺激物的重复出现称为消退。 (三)泛化与分化 泛化指在条件反射形成后的初期,另外一些类似的刺激也会引起条件反射。如狗形成了对三声铃声的条件反射(唾液分泌)后,也会对一声或二声铃声作出相同的反应,新刺激越接近原来的条件刺激,泛化现象越容易发生。 与泛化作用互补的是分化过程,就是指对事物的差异的反应。例如,狗可以学会只对三声铃声作出唾液分泌的条件反射,而对一声或两声铃声没有唾液分泌的反射。实现分化的手段可以是选择性强化或消退。 (四)二级条件作用 在已经形成的条件反射的基础上,如果将条件刺激用做无条件刺激,使它与另一个中性刺激伴随出现,就能建立一种新的条件反射,称为二级条件反射。例如,当铃声与唾液分泌的联结建立起来以后,将灯光与铃声反复伴随着(无食物)出现,经过学习,灯光也会引起狗的唾液分泌。 在二级条件反射中,有机体在建立条件反射时不再需要借助于具有生物学力量的无条件刺激(如食物)。有机体可以在已有的条件反射的基础上建立新的、更复杂的条件反射。研究二级条件反射,有助于我们理解人类的许多复杂行为。 巴普洛夫所做工作的重要性是不可估量的。他的研究公布以后不久,一些心理学家,如行为主义学派的创始人华生,开始主张一切行为都以经典性条件反射为基础。虽然在美国这一极端的看法后来并不普遍,但在俄国以经典性条件反射为基础的理论在心理学界在相当长的时间内曾占统治地位。无论如何,人们一致认为,相当一部分的行为,用经典性条件反射的观点可以作出很好的解释。 对于数学学习来说,附着力原理有一定的借鉴意义,这个原理意指一个刺激由于它刚好在某个反应之前发生而附着这个反应。这样,当这个刺激再现时,就会唤起那个反应。 在数学学习的初级阶段,“熟能生巧”的道理其实就可以归结为 巴普洛夫的经典性条件反射理论。 |
||||||||||