小学数学学习心理学

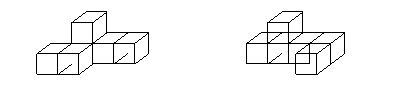
（二）把推理能力的培养落实到《标准》划分的四个领域之中

“数与代数”、“空间与图形”、“统计与概率”和“实践与综合应用”等四个领域的课程内容，都为发展学生的推理能力提供了丰富的素材。所以，数学教学必须改变培养学生推理能力的“载体”单一化（几何）的状况，要为学生提供自主探索、合作交流的时间和空间；要设置现实的、有意义的、富有挑战性的问题，引导学生参与 “过程”；要恰当的组织、指导学生的学习活动，并真正鼓励学生、尊重学生、与学生合作。这样，就能拓宽发展学生推理能力的空间，从而有效地发展学生的推理能力。

在“数与代数”的教学中，计算要依据一定的“规则”——公式、法则、运算律等，因而计算中有推理（“算理”）；现实世界中的数量关系往往有其自身的规律，用代数式、方程、不等式、函数刻画这种数量关系或变量关系的过程中，也不乏分析、判断和推理。

例1 寻找 120 的因数，不同的学生会得到不同的结果——① 12 和 10 、② 6 和 20 、③ 3 和 40 ……；他们进行讨论交流时，可能会发现这几对因数之间的关系：把①中的 12 除以 2 得 6 ，而①中的 10 乘以 2 得 20 ，即得第②对因数；第③对因数与第①、②对因数之间也有类似的关系；于是学生将会发现更多对因数：如 12 乘以 2 得 24 ， 10 除以 2 得到 5 ，发现了 120 的又一对因数 24 和 5 ……。如果学生继续探究，还能作出更一般的归纳：把一对因数中的一个因数除以某个数 ( 如果商是整数的话 ) ，另一个因数乘以这个数，就能得到一对新的因数。例如，由 210=15 × 14, 就能知道 210=5 × 42 ， 210=2 × 105 ……。在这样的过程中，学生实际上进行了简单的归纳和类比。

以上计算 |-3| 的过程，实际上是应用求一个数的绝对值的法则，进行演绎推理的过程。

（可能的猜想：个位数字与十位数字互换的两个两位数的和是个位数字与十位数字相同的一个两位数；所得的两位数能被 11 整除……）

[ 方法一：对所有的两位数一一地加以验证，但这既繁复又费时；方法二：若 a 、 b 表示一个两位数两个数位上的数字，则 ( a

10+ b )+( b

10+ a )= 11 a +11 b =11

( a+b ) ，于是”所得的两位数能被 11 整除”的猜想得到证实 ]

这样的过程，是一个经历观察、猜想、归纳、证明的过程，即既有合情推理又有演绎推理的过程。

在“空间与图形”的教学中，既要重视演绎推理，又要重视合情推理。即使在平面图形性质（定理）的教学中，也应当组织学生经历操作、观察、猜想、证明的过程，做到合情推理与演绎推理相结合（如本文前述“对顶角相等”的例子）。与原来的数学教学大纲相比，《标准》加强了三维空间几何体（立体几何）的有关内容，并为学生“利用直观进行思考”提供了较多的机会。

例4 由 6 个正方体搭成一个几何体，从正面看和左面看的图形分别为

学生在实际操作的过程中，要不断的观察、比较、分析、推理，才能得到正确的答案（以下仅提供两种答案）。这个过程不仅发展了学生的合情推理能力，而且有助于学生空间观念的形成。

“概率与统计”中的推理 ( 也称统计推断 ) 属于合情推理的范畴，是一种可能性的推理，与其他推理不同的是，由统计推理得到的结论无法用逻辑的方法去检验，只有靠实践来证实。因此，“概率与统计”的教学要重视学生经历收集、整理、分析数据、作出推断和决策的全过程。

为此，首先应由每个学生对全班同学喜欢什么样的礼物进行调查，然后把调查所得的结果整理成为数据，并进行比较，再根据处理后的数据作出决策，确定应该准备什么礼物。

这个过程中的推理，是合情推理，其结果可能只是使绝大多数同学喜欢。

再如，有一条平均水深 1.5 米的河，一个身高 1.7 米、水性不好的人下河游泳有危险吗？学生在对”平均水深”有了很好的理解之后，会得到这样的结论：可能有危险，这又是进行合情推理得到的结果。

例6 我国的高考一般都安排在每年 7 月的 7 、 8 、 9 日三天，考虑到天气等原因，经过专家的论证，认为将高考的时间提前一个月比较合适。为了了解学生对此的看法，某教育行政部门对某中学高三年级某班的学生进行了调查，调查结果为：不到 20% 的学生赞成，不到 30% 的学生“无所谓”，其余的学生不赞成。请你谈谈对这个调查结果的看法。

掌握了基本的统计知识和方法的学生，经过思考、分析就可能对教育行政部门调查所得到的结果提出质疑。因为这样选取调查的样本，无论从数量上还是随机性方面都不能很好地代表总体，所以由此得到的统计推断的可靠性很小。

（三）在学生的日常生活、游戏活动中发展学生的推理能力

毫无疑问，学校的教育教学（包括数学教学）活动能推进学生推理能力更好地发展。但是，除了学校教育以外，还有很多活动也能有效地发展人的推理能力。例如，人们在日常生活中经常需要作出判断和推理，许多游戏活动也隐含着推理的要求……等。所以，要进一步拓宽发展学生推理能力的渠道，使学生感受到生活、活动中有“学习”，养成善于观察、勤于思考的习惯。

例如，两个人握一次手；若每两人握一次手，则三个人共握几次手？ n 个人共握多少次手呢？（通过合情推理探索规律）

这与“由上海开往北京的 1462 次列车途中停靠 23 个站（不包括上海和北京），这次列车共发售多少种不同的车票”这样的问题，有什么联系呢？（类比）

像图（ 1 ）、（ 2 ）、（ 3 ）这样铺下去，第 n 个图形中有多少块彩色水泥砖？假设每块正方形水泥砖的长度为 20 ㎝，那么铺设 1 Km 长的人行道需要多少块彩色水泥砖？

再观察铺地所用的地砖不仅可以是正方形的，也可以是三角形的……，那么用五边形的地砖能够没有缝隙、又不重叠的铺地吗？

又如，给林老师家打电话，若振铃多次都无人接听，则常常由此作出 “ 林老师不在家”的判断。这种判断隐含了反证法的思想。

商店介绍某种品牌的桂圆说：“××牌桂圆颗颗圆而大，肉质厚而甜”。一位消费者从一堆桂圆中挑出了一颗小的桂圆后，对营业员说：“你说的话不真实”。这就是用举“反例”的方式证明结论不成立。

此外，还可以设计一些游戏，让学生在在有趣的活动中学习推理。比如，甲、乙、丙三人戴红、黄、白三种颜色的帽子：

① 甲说：“我不要红帽子”；乙说：“我不要黄帽子”；丙说：“我不要白帽子”。如果三人的要求都得到满足，那么猜猜他们分别戴了什么颜色的帽子？

（有两种可能：甲、乙、丙分别戴黄、白、红或白、红、黄颜色的帽子）

② 甲说：“我要黄帽子”；乙说：“我不要黄帽子”；丙说：“我不要白帽子”。如果三人中只有一人的要求得到满足，那么猜猜他们分别戴了什么颜色的帽子？

（解答：甲戴白帽子，乙戴黄帽子，丙戴红帽子。推理过程如下：

若甲的要求得到满足，即甲戴黄帽子，则乙就不可能再戴黄帽子，乙的要求同时就得到满足。这与”只有一人的要求得到满足”矛盾。

若乙的要求得到满足，即乙不戴黄帽子，则由于此时甲的要求不能再得到满足，因而甲也不戴黄帽子，所以只能丙戴黄帽子；这样丙的要求却得到了满足。这也与”只有一人的要求得到满足”矛盾。

若丙的要求得到满足，即丙不戴白帽子，则由于此时乙的要求不能再得到满足，因而乙戴黄帽子；于是可知丙戴红帽子，甲戴白帽子。这样，甲、乙的要求都没有得到满足，只有丙的要求得到满足。）

《标准》十分强调：数学教学要紧密联系学生的生活实际，从学生的生活经验和已有知识（从学生的实际）出发。推理能力的培养，必须充分考虑学生的身心特点和认知水平，注意层次性。

一般地说，操作、实验、观察、猜想等活动的难易程度容易把握，所以合情推理能力的培养应贯穿于义务阶段教学的始终。即使如此，《标准》在“学段目标”的“数学思考”部分的表述中，三个学段仍然有着一定的层次：例如，“在教师的帮助下，初步学会选择有用信息进行简单的归纳和类比（第一学段）”；“能根据解决问题的需要，收集有用的信息，进行归纳、类比与猜测，发展初步的合情推理能力（第二学段）”；“能收集、选择、处理数学信息，并作出合理的推断或大胆的猜测”，“能用实例对一些数学猜想作出检验，从而增加猜想的可信程度或推翻猜想（第三学段）”……。

三个学段培养学生演绎推理能力则应更好地体现层次性。《标准》在第一、第二学段中，并没有对此提出具体的要求，而是要求学生“能进行简单的、有条理的思考”、“能进行有条理的思考，能对结论的合理性作出有说服力的说明”；《标准》在第三学段才明确提出“体会证明的必要性，发展初步的演绎推理能力”的要求。

例如，“空间与图形”的学习，不同学段的学生观察、实验、推理的方式是不同的。在第一、二学段，学生主要通过简单的“看”、“摆”、“拼”、“折”、“画”等实践活动，感知图形的性质，或归纳得到一些结论；而到了第三学段，在各种形式的实践活动中探索得到的结论，有时需要运用演绎推理的方式加以证明。如“画一个角等于已知角”的教学，大体经历这样的过程：用量角器、三角板画角，按照一定的步骤会用尺规画角——用重合的方法直观地感知所画的角等于已知角——学习了三角形的全等判别条件后，则可以用演绎推理的方式 ( 利用“边、边、边”的全等条件 ) 证明所画的角与已知角相等。

应当指出：培养学生的演绎推理能力不仅要注意层次性，而且要关注学生的差异。要使每一个学生都能体会证明的必要性，从而使学习演绎推理成为学生的自觉要求，克服“为了证明而证明”的盲目性；又要注意推理论证“量”的控制，以及要求的有序、适度。