|
章节导航 |
|||||
|
绪 论 第一章 第二章
第一节 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章 |
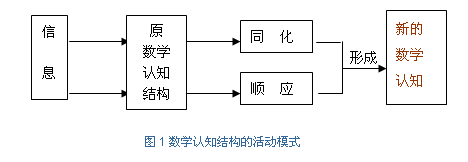
四、数学认知结构的基本特点 数学认知结构有如下几个特点: (一)数学认知结构是数学知识结构与学生心理结构相互作用的产物。 学生的数学认知结构是由教材知识结构转化而来的,它保留了数学知识结构的抽象性和逻辑性等特点,又融进了学生感知、理解、记忆、思维和想象等心理特点,它是科学的数学知识结构与学生心理结构相互作用、协调发展的结果。 在其发展过程中两者表现出互相影响、互相促进、辩证统一的发展态势:一方面,数学知识结构直接影响着学生心理结构的发展,不仅规定着数学认知结构的内容和发展方向,同时还制约着学生感知、理解等心理活动的过程和方式;另一方面学生的心理结构又不断地改造着数学知识结构,使数学知识结构变成与他们心理发展水平和认知特点相适应的数学认知结构。 正是由于学生心理结构对数学知识结构的主观改造,导致了学生数学认知结构的个体差异。 (二)数学认知结构是学生已有数学知识、经验在头脑里的组织形式。 从学生构建数学认知结构的过程和方式来看,他们都是以原有知识为基础对新的数学知识进行加工改造或者适当调整自己的数学认知结构,然后按照一定的方式将所要学习的新知识内化到头脑里,使新旧内容融为一体,形成相应的数学认知结构,并通过这种形式把所学数学知识储存下来的。 由此表明,就其形态而言,数学认知结构又是学生已获得的数学知识和数学经验在头脑里的组织形式,这种组织形式反映了数学知识内化到学生头脑里以后的结构状态。 有关研究表明,数学认知结构在学生头脑里是呈板块结构的。具体来讲,源源不断的新知识内化到头脑里以后,在新旧内容相互作用的基础上,学生将所掌握的数学知识形成若干系统,由此在头脑里组成相应的数学知识板块,板块的大小和多少直接受所学数学知识内容的多少的制约和影响。呈板块结构状态的数学知识既便于储存,又便于提取。 (三)数学认知结构是一个不断发展变化的动态结构。 由于学生的数学认知结构是在后天的学习活动中逐步形成和发展起来的,所以它又是一个不断发展变化的动态结构,其动态性主要表现在以下几个方面: 1. 数学认知结构的建立要经历一个逐步巩固的发展过程。对某一具体数学知识的学习来说,学习初期,学生在老师的帮助下通过原有认知结构和新知识的相互作用,只能在头脑里形成相应数学认知结构的雏形,其结构极不稳定,需要紧跟其后的有效练习和在后继内容学习中的进一步应用,所形成的数学认知结构才能逐步巩固和稳定。 2. 学生头脑里的数学认知结构经过不断分化逐步趋于精确。学习初期学生头脑里形成的数学认知结构是笼统的,甚至是模糊的,随着认知活动的不断深入,他们头脑里的数学知识经过不断分化才能形成比较精确的数学认知结构。 如学习三角形,学生首先获得的是“由三条线段围成的封闭图形”、“三角形有三条边、三个角”的笼统认识。随着学习过程的不断深入。学生会逐步发现:就角来讲,三角形可以分为锐角三角形、直角三角形、钝角三角形;从边来看,三角形有等边三角形、等腰三角形和不等边三角形。这一过程的完成,标志着学生对三角形有了比较精确的认识。 3. 学生的数学认知结构是逐步扩充和完善的。随着学习过程的逐步深入和数学知识的不断积累,学生的数学认知结构将会随之不断地扩充和完善。 如有关整数乘法的认知结构,在二年级学生仅形成了一位数乘一位数(即表内乘法)的认知结构,在三年级又分别形成了一位数乘多位数和两位数乘多位数的认知结构,在四年级又进一步形成了三、四位数乘法的认知结构。经过三年级的系统学习,学生最终才在头脑里形成了一个相对完善的整数乘法认知结构,每次新的学习对学生原有认知结构来说都是一次新的扩充。 (四)数学认知结构是一个多层次的组织系统。 数学认知结构是一个相对的概念,它的内容是一个多层次的庞大系统。既可以是大到包括整个小学数学知识系统在内的数学认知结构,也可以是小到由一个概念或命题组成的数学认知结构。 数学认知结构的层次性主要是由数学知识结构内部的层次性和逻辑系统性决定的,原则上数学知识有怎样的分类,学生的数学认知结构就有怎样的划分。 如分数可以分为真分数和假分数,假分数又可以分为整数和带分数,相应地学生头脑里的分数认知结构在层次上也可作出相应的划分。 数学认知结构的层次性还体现在认知结构的发展水平上,对小学生来讲既有直观水平上的数学认知结构,也有抽象化水平上的数学认知结构。 (五)每一个学生的数学认知结构各有其特点。 数学认知结构受多种心理因素的影响,每个学生的认知方式和认知水平表现出很大的差异,因而他们的认知结构往往表现出自身的个性特征。例如,有的学生习惯于知识经验的纵向组织,有的则偏重于横向的编排;有的学生善于知识经验的概括和整理,有的则习惯于知识的堆积,所以学生认知结构的状况往往因人而异,从而导致了他们在学习上的差异。 (六)数学认知结构是一个积极的组织,它在数学认知活动中,乃至一般的认知活动中发挥作用。 数学认知结构在数学认知活动中,乃至一般的认知活动中发挥着主动的作用。形成了一定的数学认知结构后,一旦出现新的数学信息,人们总是立即用相应的数学认知结构对所面临的信息进行科学的加工处理,从而表现出数学认知结构的能动性,这种活动如图 1 所示:同化和顺应是学生原有数学认知结构和新的学习内容相互作用的两种基本形式。
(七)数学认知结构是在数学认知活动中形成和发展起来的。 数学认知结构是学生数学学习过程中的一个中心的心理成份,是在数学认知活动中形成和发展起来的,随着认知活动的不断进行和学生认知水平的逐步提高,学生的数学认知结构将不断被分化和重组,并逐渐达到精确化和完善化的程度。 |
||||
第三章 |
第一节 数学认知结构 |
第二节 数学学习过程的一般模式 一、数学学习过程的一般模式 |